R1 2012 høst LØSNING
Del 1
Oppgave 1
a)
$f(x)=(2x-1)^2 = 4x^2-4x+1$
Da er
<math>f^\prime(x)=8x-4</math>
Alternativt kan vi benytte kjerneregelen med $2x-1$ som kjerne. Vi får da
$f^\prime(x) = 2(2x-1) \cdot (2x-1)^\prime = 2 \cdot (2x-1) \cdot 2 = 8x - 4$.
b)
<math>g(x)=\sqrt{x^2-2x}</math>
Vi bruker kjerneregelen med <math>x^2 - 2x</math> som kjerne. Da har vi
<math>\begin{eqnarray*} g(x) &=&\frac{1}{2\sqrt{x^2 - 2x}} \cdot (x^2 - 2x)^\prime = \frac{1}{2\sqrt{x^2 - 2x}} \cdot (2x-2) \\ &=& \frac{x-1}{\sqrt{x^2-2x}}\end{eqnarray*}</math>
c)
Her har vi et produkt av flere faktorer som avhenger av $x$. Da benytter vi produktregelen. For å derivere $e^{3x}$ bruker vi også kjerneregelen. Vi får
$h^\prime(x) = (x^3)^\prime \cdot e^{2x} + x^3 \cdot (e^{2x})^\prime = 3x^2 e^{2x} + x^3 \cdot 2e^{2x} = x^2e^{2x}(3+2x).$
Oppgave 2
a)
En polynomdivisjon $p(x) : (x-a)$ går opp kun dersom $p(a) = 0$. Her får vi da at $f(3)$ må være 0. Det gir oss ligningen
$f(3) = 0 \ \Leftrightarrow \ 3^3 - 3 \cdot 3^2 + k \cdot 3 + 3 = 0 \ \Leftrightarrow \ 3k + 3 = 0 \ \Leftrightarrow \ k = -1.$
b)
Svaret på polynomdivisjon = <math>x^2-1</math>
Dette gir oss førstegradsfaktorer i (x-1)(x+1)(x-3)
Oppgave 3
a)
Vendepunkt har vi der den dobbeltderiverte er 0 og skifter fortegn. Vi har her
<math>f(x)=x^3-3x^2-x+3</math>
<math>f^\prime(x)=3x^2-6x-1</math>
<math>f^{\prime\prime}(x)=6x-6 = 6(x-1)</math>
Den dobbeltderiverte er null for x = 1. Vendepunkt: (1, f(1)) = (1, 0)
b)
Likning for vendetangent: f ' (1) = - 4
y = ax + b
Har punktet (1, 0) og setter inn:
$0 = -4 \cdot 1 +b \\ b = 4 $
Dvs: y = -4x + 4
Oppgave 4
a)
x = 1 er en løsning av likningen. Elven mister en løsning ved ikke å sjekke faktoren (x-1) lik null.
b)
For å finne skjæringspunktet må man sette $f(x)=g(x)$
$(x-1)(x-3)=x-1$
<math>x^2-4x+3=x-1</math> => <math>x^2-5x+4=0</math>, deretter bruker man ABC-formelen for å finne nullpunktene.
Nullpunktene er; $x=4$ og $x=1$
For å finne skjæringspunktene setter man $f(4)$ og $g(1)$. Da finner man en y-verdi. $f(4)=(4-1)(4-3)$ $f(4)=3$, noe som betyr at $y=3$
$g(1)=1-1=0$, noe som betyr at $y=0$.
Skjæringspunktene ligger i punktene $(4,3)$ og $(1,0)$
Oppgave 5
a)
$AB = \vec v \\ AD = \vec u \\ AC = \vec u + \vec v \\ BD = \vec u - \vec v \\ \vec{AC} \cdot \vec{BD }= (\vec u + \vec v ) \cdot (\vec u - \vec v ) \\ \vec {u^2} - \vec{v^2} =0$
Siden skalarproduktet mellom vektorene er null, står de vinkelrett på hverandre.
b)
$A_{\Box ABCD} = A_{\triangle ABC} + A_{\triangle ACD} \\ \frac 12 AC \cdot FB + \frac 12 AC \cdot DF \\ \frac 12 AC (FB + DF) \\ \frac 12 AC \cdot BD$
Oppgave 6
a)
$3^{4x}+7=34 \\ 3^{4x}=27 \\ 3^{4x}=3^3 \\ lg3^{4x}= lg3^3 \\ 4x = 3 \\ x = \frac 34 $
b)
$lg(x) + lg (x-1) = lg 2 \quad x>1 \\ lg(x^2-x)= lg2 \\ x^2-x = 2 \\ x^2 - x - 2 =0 \\ x =\frac{1 \pm \sqrt{1+8}}{2} \\ x= -1 \vee x=2 $
Oppgave 7
a)
Vinkel er 90 grader kun når skalarproduktet mellom vinkelbeina er null, bare da.
Dvs: $\vec{AB} \cdot \vec{AC} =0$
$ \vec{AB} =[7-3, 3-0] = [4,3] \\ \vec{AC} = [0-3, t-0]= [-3, t] \\ \vec{AB} \cdot \vec{AC} = 0 \\ 4(-3) +3t =0 \\ t =4 \\ \angle BAC = 90 ^{\circ} \quad når \quad t = 4 $
b)
Avstanden fra punktet A (3,0) til vektoren BC = [-7,1] :
Korteste vei fra A til BC er til et punkt D på BC som er slik at AD er normalt på BC.
$ \vec{AD} = \vec{AB} + k \vec{BC} \\ \vec{AD} = [4,3] +k[-7,1] \\ \vec{AD}=[-7k+4,k+3] \\ \vec{AD} \perp \vec{BC} \\ [-7k+4,k+3] \cdot [-7,1] =0 \\ 49k -28 +k +3=0 \\ 50k =25 \\ k= \frac 12 \\ \vec{AD} = [-7 \cdot \frac 12 + 4, \frac 12+3] = [\frac 12, \frac{7}{2}] \\ | \vec{AD} | = \sqrt{\frac 14 + \frac{49}{4}} = \frac{\sqrt{50}}{2} = \frac{5 \sqrt 2}{2}$
Avstanden fra A til BC er fem halve kvadratroten av to.
DEL 2
Oppgave 1
a)
$\vec{AC} = [4, 4] \quad \quad | \vec{AC}| = \sqrt{4^2+4^2} = \sqrt{32} \\ \vec{AB} =[6, 0]\quad \quad | \vec{AB}| = 6 \\ \vec{AB} \cdot \vec{AC} = 0 \cdot 4 + 6 \cdot 4 = 24 $
Skalarprodukt:
$\vec{AB} \cdot \vec{AC} = |\vec{AB}|\cdot |{AC}| \cdot \angle CAB \Rightarrow \angle CAB = \frac{vec{AB} \cdot \vec{AC}}{|\vec{AB}|\cdot |{AC}|} = \frac{24}{6 \sqrt{32}} = \frac{1}{\sqrt2} = \frac{\sqrt 2}{2} \\ \angle CAB = 45^{\circ}$
b)
Dersom firkanten er et parallellogram er BC vektor lik AD vektor.
$ \vec{BC} = [-2, 4] \\ \vec{AD} = [t, 4] \\ [t,4] = [-2,4] $
Innspeksjon viser oss at t = -2 gjør firkanten ABCD til et parallellogram.
c)
$ AC \perp BD \Leftrightarrow \vec{AC} \cdot \vec{BD} = 0 \\ \vec{BD} = [t-6, 4] \\ \vec{AC} \cdot \vec{BD} = 0 \\ [4,4] \cdot [t-6, 4] = 0 \\ 4t-24+16=0 \\ t=2$
Når t = 2 står AC vinkelrett på BD.
Oppgave 2
a)
| Gutter | Jenter | Totalt | |
|---|---|---|---|
| Buss | 71 | 94 | 165 |
| Ikke Buss | 111 | 74 | 185 |
| Total | 182 | 168 | 350 |
Sannsynlighet for jente og buss:
$P(J \cap B) = \frac{94}{350} =0,27$
b)
Sannsynlighet for buss:
$P(B) = \frac{165}{350} = 0,47 \\ $
Sannsynlighet for buss når man vet at eleven er jente:
$P(B|J)= \frac {94}{168} = 0,56$
$P(B) \neq P(B|J)$ derfor er hendelsene B og J avhengige.
c)
$P(J|B) = \frac{94}{165} = 0,57$
Her kunne man også brukt Bayes' formel, men siden alle tall er oppstilt i krysstabellen er regning ikke nødvendig.
Oppgave 3
a)
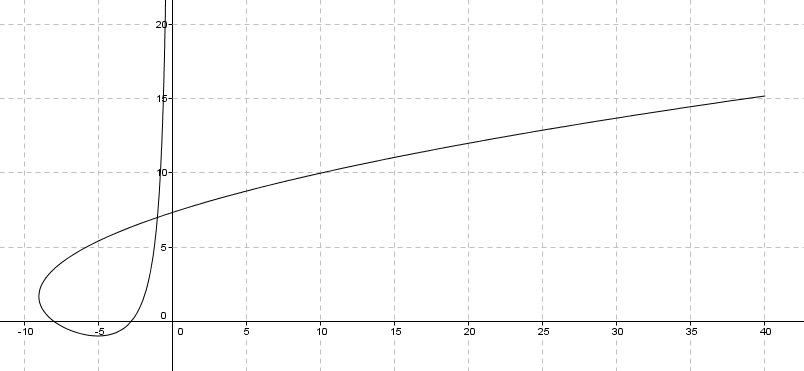
$\vec r (t) =[ \frac 14 t^2 - 3t, t + \frac 4t - 5], \quad t \in <0,20]$
b)
Skjæring med y- akse inntreffer når x(t) = 0.
$ \frac 14t^2-3t=0 \\ t^2-12t =0 \\ t(t-12)=0 \\ t= 0 \vee t=12$
t = 0 er en ugyldig verdi og vi har bare ett skjæringspunkt:
$ (0,y(12)) = (0, 12+ \frac {4}{12} - 5) = (0, \frac{22}{3} )$
Skjæring med x- aksen inntreffer når y(t) = 0:
$t + \frac 4t-5 =0 \\ t^2 - 5t + 4 =0 \\ x= \frac{5 \pm \sqrt{(-5)^2 - 16}}{2}\\ t = 1 \vee t =4$
c)
Banefarten etter t sekunder er gitt ved:
$| \vec {v}(t)| = | \vec{r}'(t)| = | [ \frac12t-3, 1 - \frac{4}{t^2}]| \\ | \vec v(5)| = |[\frac 12 \cdot5-3,1-\frac{4}{5^2}] |= \sqrt{(- \frac12)^2+ ( \frac{21}{25})^2} =0,978$
Etter 5 sekunder er banefarten 0,978
Oppgave 4
a)
Trekantene er formlike. Vinkel C er felles i begge trekantene. DE er parallell med AB, derfor er vinkel CDE lik vinkel CAB og vinkel CED lik vinkel CBA.
$\frac{8-h}{8} = \frac x6 \\ 8-h = \frac {8x}{6} \\h = 8 -\frac 43x$
b)
Areal av trekanten DEF:
$T(x) = \frac{Gh}{2} = \frac{x(8- \frac43x)}{2} = 4x - \frac 23x^2$
c)
$T ´(x) = 4- \frac 43x \\ T ´(x) = 0 \\ x=3$
T har sin største verdi når x = 3. Vi ser at dette er et toppunkt siden faktoren i andregradsleddet er negativ.
$T(3) = 4 \cdot 3 - \frac 23\cdot 3^2 = 12-6 = 6$
Det største arealet er 6.
Alle fire trekantene er likebeinte og har en side med lengde 3 og høyde 4. Derfor er trekantene kongruente.
Oppgave 5
a)
$x^2-2x+y^2+4y-4=0 \\ (x^2-2x+1)+(y^2+4y+4) ) = 1+8 \\ (x-1)^2 + ((y+2)^2 = 9$
Radius i sirkelen er 3. Sentrum er (1, -2).
b)
$x^2+2tx +y^2-4y +9 =0 \\ (x^2 + 2tx + t^2) + (y^2 - 4y + 4) = t^2 -5 \\ (x+t)^2 + (y-2)^2 =t^2-5 $
Dersom sirkelpereferien har kun ett punkt felles med x - aksen betyr det at den tangerer, altså at y kooedinaten er lik radiusen.
$4= t^2-5 \\t^2-9 =0 \\ t = -3 \vee t=3$
For at sirkelen skal tangere xáksen må t være lik -3 eller 3.
Oppgave 6
a)
Her må du vite hva en pereferivinkel og en sentralvinkel er. v er 90 grader. Da er BAC 45 grader. ACD er 60 grader, ADC er 90, da må CAD være 30. BAD blir da 45 + 30 grader, altså 75 grader.
b)
$\alpha = 180^{\circ} - \angle BAP - \angle PBA =180^{\circ}-75^{\circ}- 90^{\circ} = 15^{\circ} \\ \beta= 180^{\circ} - \angle QAD - \angle QDA=180^{\circ}-75^{\circ}- 90^{\circ} = 15^{\circ} $
c)
De to trekantene har en felles vinkel i A. Videre thar de to trekantene begge en pereferivinkel som spenner over diameteren, i B og D. Vinkelsummen er konstant lik 180 grader . $\alpha$ og $\beta$ vil derfor være like for alle verdier av u og v.