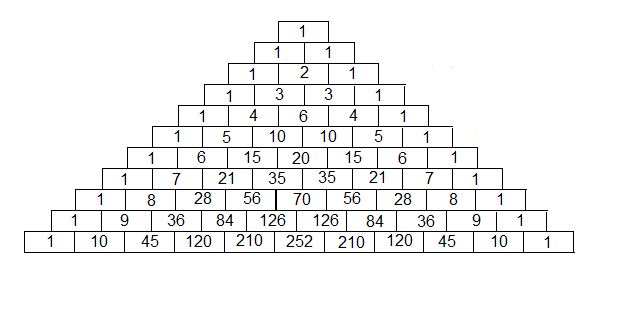
Pascals talltrekant

Pascalls talltrekant viser mange interesante sammenhenger. Vi ser på noen av dem her.

Hvordan bygge opp trekanten?

Tallet en står øverst, i NULLTE rad. Under kommer to enere i første rad, 1,2,1 i andre rad, osv. Langs sidene er det enere. Et tall i trekanten er summen av de to tallene på raden over. Tallene 10 på rad fem er summen 4+6 på rad fire, rett over.

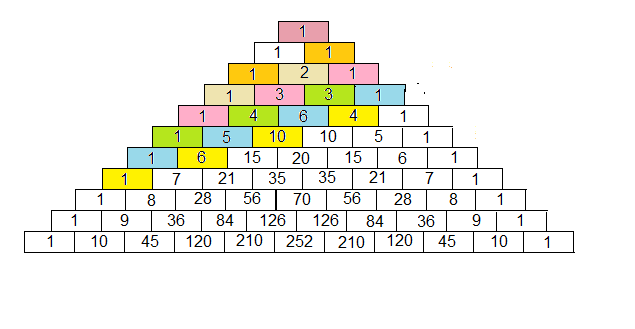
Mønster i trekanten

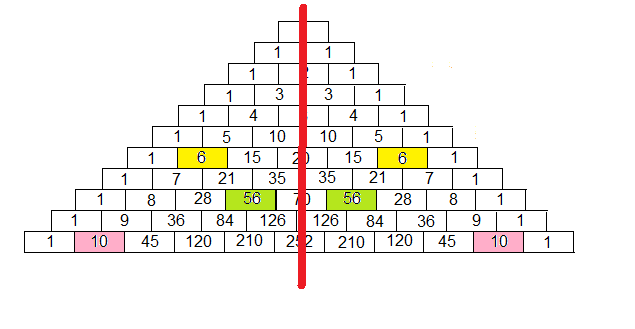
Symmetri

Kvadrater

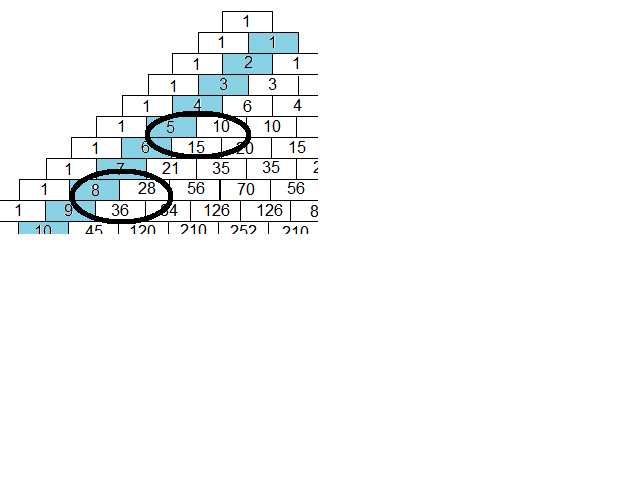$5^2 = 15+10 =25 \\ 8^2 = 28+36= 64$

Naturlige tall

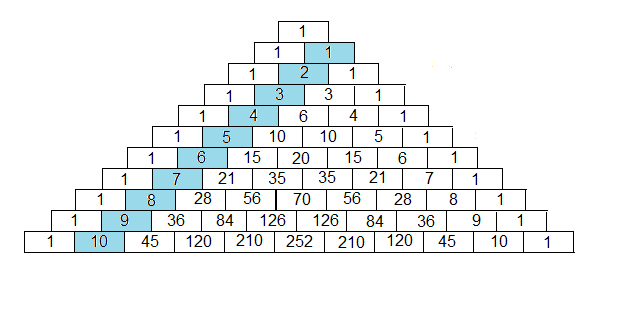
Trekanttall

Tallene i tredje diagonal er det vi kaller for trekanttallene.

Horisontale summer

Dersom man summerer de horisontale radene i trekanten får man:

$1 = 2^0 \\ 1+1 =2 = 2^1 \\1+2+1=4 =2^2\\ 1+3+3+1 = 8 =2^3 \\ 1+4+6+4+1 = 16 =2^4 \\1+5+10+10+5+1 =32 = 2^5$

osv.

Man observerer at alle horisontale summer er potenser av to.

Fibonacci

Begynn på toppen. Gå en opp og en til høyre. Gå en ned langs venstre kant og gjør det samme.

1 +1 + (1+1)+ (1+2) + (1+3+1) + (1+4+3) + (1+5+6+1) + (1+6+10+4) + ..... = 1 + 1 + 2 + 3 + 5 + 8+ 13 + 21+ ......

Fibonacci rekken starter med tallene 1 og 1 og det neste tallet er summen av de to foran.

Polynomer

$ (x+1)^0 =$ 1

$ (x+1)^1 =$1 x+1

$(x+1)^2 =$ 1$x^2$+2x+1

$(x+1)^3$ = 1$x^3$+3$x^2$+3x+1

$(x+1)^4$ = 1$x^4$+4$x^3$+6$x^2$+4 x +1

Binominal koeffisienter

Velg k elementer av n elementer. Hvor mange muligheter finnes? $\dbinom{n}{k} = \frac{n!}{k!(n-k)!}$

$\dbinom{0}{0} \\ \dbinom{1}{0} \dbinom{1}{1} \\ \dbinom{2}{0} \dbinom{2}{1} \dbinom{2}{2} \\ \dbinom{3}{0} \dbinom{3}{1} \dbinom{3}{2} \dbinom{3}{3} \\ \dbinom{4}{0} \dbinom{4}{1} \dbinom{4}{2} \dbinom{4}{3} \dbinom{4}{4} $