Parameterfremstilling

Innledning

Parameterfremstilling er en måte å fremstille kurver på ved hjelp av en ”hjelpevariabel”. En parameter er en variabel. Parameterframstilling er nyttig i mange tilfeller, for eksempel dersom et objekt beveger seg som funksjon av tiden. Det er nødvendig å være fortrolig med vektorregning.

I planet

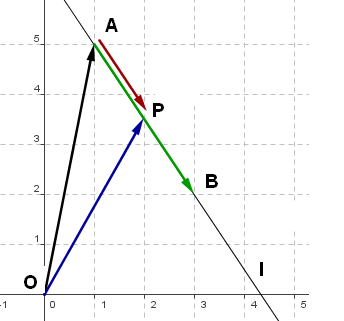
La <math> \vec{AB} </math> være en vektor paralell med linjen l. Velg et vilkårlig punkt P på l. <math> \vec{OP} </math> kan uttrykkes som <math> \vec{OA} + \vec{AP} </math> .

<math> \vec{AP} </math>er parallell med <math> \vec{AB} </math> derfor er<math> \vec{AP} = t\vec{AB} </math> .

Man får:<math> \vec{OP} = \vec{OA} + t\vec{AB} </math>

Et hvilken som helst punkt på linjen l kan uttrykkes på denne måten, ved å variere t.

Parameterframstilling av en rett linje

For å framstille en rett linje ved parameterframstilling trenger man et punkt på linja og retnigsvektoren. Begge deler er gitt dersom man kjenner to punkter på linjen, eller likningen for linjen (to sider av samme sak). Siden en linje består av uendelig mange punkter og har uendelig mange retningsvektorer er det uendelig mange måter for parameterfremstillingen. Det er vanlig å velge punkt og vektor slik at fremstillingen blir enklest mulig. Poenget er at to tilsynelatende forskjellige fremstillinger kan begge være riktige.

f(x) = ax + b

Rettningsvektor til f(x) er [1,a]

Dersom f(x) går gjennom punktet <math>(x_0,y_0)</math> blir parameterframstillingen for linjen

l: <math>[x_0,y_0] + t[1,a]</math>

som gir:

<math> \left [ x = x_0 +t \\ y = y_0 + at \right]</math>

Som også kan skrives:

l:<math> \left [x = f(t) \\ y = g(t) \right]</math>

på en mer generell form.

Eks. 1:

Finn parameterframstillingen for linjen m som går gjennom punktet (2,1) og som er parallell med linjen y= 2x – 1

LØSNING:

Rettningsvektor er [1,2].

Man får: m: [2,1] + s[1,2] som gir:

m:<math>\left [x = 2+s \\ y = 1 + 2s \right ]</math>

som er en parameterfremstilling for m, med s som parameter.

Eks. 2:

Finn parameterfremstillingen for en linje som går gjennom punktene (2,3) og (4, -2).

LØSNING:

Rettningsvektor blir [4-2,-2-3] = [2,-5]. Velger [2,3] som <math>\vec{OA}</math> og får:

<math>\left [x = 2+2t \\ y = 3-5t \right ] </math>

Eks. 3:

Finn parameterframstillingen for en linje m som står vinkelrett på linjen y = - 0,5x + 5 og som går gjennom punktet <math> ( - \frac{3}{2}, \frac 14)</math>.

LØSNING:

En linje vinkelrett på y kan ha rettningsvektor [1,2].

Man får:

m: <math> \left[ x= - \frac{3}{2} + s \\ y= \frac 14 + 2s \right]</math>

Eks.4

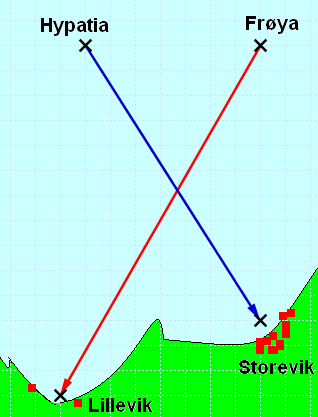
To båter, ”Frøya” og ”Hypatia,” har ved tiden t =0 posisjon og kurs som figuren over viser.

Avstanden mellom båtene ved tiden t =0 er 7 nautiske mil. En nautisk mil er 1852 meter.

a) Finn en parameterframstilling for båtenes kurser. Du legger selv inn et koordinatsystem i kartet.

b) Finn koordinatene til skjæringspunktet mellom båtenes kurs.

c) Dersom båtene holder samme fart vil de da kollidere?

d) Hvilken båt kommer først til skjæringspunktet mellom kursene?

e) Hva er avstanden mellom båtene da?

LØSNING:

a) Man legger inn et koordinatsystem i kartet, for eksempel med origo i Hypatia, ved tiden t=0. Det gir følgende koordinater i startøyeblikket.

Hypatia ( 0,0)

Frøya (7,0)

Lillevik (-1, -14)

Storevik (7, -11)

Kursene båtene følger på parameterform:

Hypatia:

Frøya:

b) Når kursene krysses må begge x koordinater være like, og begge y koordinater være like:

7t = 7 - 8s og -11t = -14 s

som gir S= 0,414 og t = 0,527

Innsatt i en av parameterframstillingene gir det koordinatene til kryssningspunktet:

x = 3,69 og y = -5,80

c) Siden båtene holder samme fart er det avstanden fram til kryssningspunktet som avgjør om de vil kolidere. Avstanden finne ved pytagoras:

Hypatia: 6,8 nautiske mil

Frøya: 6,7 nautiske mil

Det vil være en avstand på ca. 0,1 nautisk mil, altså ca. 200 meter, noe som for større båter vil kunne skape en farlig situasjon. Frøya kommer først til punktet.