Likninger av første grad, med en, to, og tre ukjente
Innledning
I matematikk er det vanlig å bruke bokstaver som erstatning for tallverdier. Bokstaver kan symbolisere tall som vi kjenner, for eksempel π som har tallverdi 3,14. Bokstavene kan også symbolisere tallverdier som vi ikke kjenner, men som vi ønsker å finne. I slike tilfeller bruker vi gjerne bokstavene x, y eller z.
En Ukjent
I et spesielt regnestykke kan x kun ha en tallverdi, men x kan ha forskjellige verdier i forskjellige regnestykker.
La oss se på noen eksempler:
Per og Kari har til sammen 5 epler. Per har to. Hvor mange har Kari?
Dette stykket greier du sikkert i hodet, men la oss sette det opp som en ligning slik at vi lærer oss tenkemåten. La oss kalle antall epler som Kari har for x.
Per + Kari = tilsammen
2 + ? = 5
Som likning kan dette skrives:
2 + x = 5
Tenk på en skålvekt. En skålvekt er i likevekt dersom lasten er den samme i begge skålene. Vi kan legge på mer last på vekten, men for at den skal være i likevekt må vi legge like mye i begge skålene. Vi kan også fjerne last fra skålvekten, men vi må fjerne like mye fra begge skålene for at likevekten skal holde seg. Gjør vi ikke det kommer vekten ut av balanse.
Tenk deg at likhetstegnet i vår ligning er balansepunktet på skålvekten. Vi kan legge til og trekke fra på begge sider, vi kan gange og dele, men det er viktig at vi gjør det samme på begge sider av likhetstegnet. Gjør vi ikke det kommer "vekten" ut av balanse.
Situasjonen med Per og Kari ser slik ut:

Karis epler befinner seg i sekken. Vår oppgave er å finne antall epler i sekken, x.
Dersom vi fjerner to epler på hver side av skålvekten ser det slik ut:
På matematikkspråk kan vi skrive det slik:
2 + x = 5
Dersom vi trekker bort to fra hver side av likhetstegnet får vi:
2 + x - 2 = 5 - 2
x = 5 - 2
x = 3
"flytt og bytt" er en huskeregel, men det er viktig å forstå at man trekker fra samme tall på begge sider av likhetstegnet.
Med "flytt og bytt" mener man at man flytter leddet som ikke inneholder x over på høyre side av likhetstegnet og bytter fortegn. Likedan kan man flytte ledd som inneholder x fra høyre til venstre side av likhetstegnet og skifte fortegn. Det man i virkeligheten gjør er å trekke fra like mange på hver side.
Når vi løser en ligning er det vår oppgave å få x alene på venstre side av likhetstegnet.
Omvendte operasjoner
- Addisjon og subtraksjon opphever hverandre.
- Multiplikasjon og divisjon opphever hverandre.
- Operasjonene må utføres på alle ledd i likningen, på begge sider av likhetstegnet.
Ligning med x som ledd
Man flytter alle ledd med x på venstre side og alle ledd uten x på høyre side av likhetstegnet. Husk å bytt fortegn på de ledd som flyttes. Trekk sammen på begge sider av likhetstegnet.
Eksempel 1:
<math> x = 2 </math>
Ligning med x som faktor
Løsningen er å dividere alle ledd på begge sider av likhetstegnet med tallet som står foran x.
Eksempel 2:
<math>5x = x + 8 \quad \quad</math> Flytter over x på venstre side og skifter fortegn.
<math> 5x - x = 8 \quad \quad</math> Trekker sammen
<math> 4x = 8 \quad|:4 \quad \quad</math>Deler begge sider av likhetstegnet på det tallet som står forran x, i dette tilfelle 4.
<math> x = 2 </math>
Ligninger med x i teller
Løsningen er å multiplisere alle ledd på begge sider av likhetstegnet med tallet i nevner.
Eksempel 3:
Ligninger med x i nevner
Løsningen er å multiplisere alle ledd på begge sider av likhetstegnet med x.
Eksempel 4:
2 + 10x = 12x $\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad $ Flytt over og bytt fortegn
-2x = -2
x = 1
Kombinasjoner av metoder
Ofte vil ligningene du løser være en kombinasjon av metodene over:
Eksempel 5:
<math> x = \frac12 </math>
Prøve på Svaret
Hvordan kan vi være sikre på at utregningene i eksemplet over er riktige? Et godt hjelpemiddel er å sette prøve på svaret. Det betyr at vi setter inn den x verdien vi har funnet i ligningen. Vi behandle hver side av likhetstegnet for seg. Dersom svaret vi får blir det samme på begge sider av likhetstegnet har vi med stor sannsynlighet regnet riktig.
Vi tester svaret over:
Eksempel 6
<math>VS: \qquad \qquad 3 \cdot \frac12 + \frac{\frac12}{2} = \frac32 + \frac 14 = \frac 74 </math>
<math>HS:\qquad \qquad 4 - \frac{2}{\frac12} + \frac{7\cdot \frac12}{2}= 4 - 4 + \frac74 = \frac74</math>
Vi ser at vi får det samme på begge sider og kan konkludere med at x verdien vi fant er riktig.
Gjør det til en regel at du setter prøve på svaret, selv om det ikke alltid spørres etter det.
Dagligdags Bruk - tekststykker
Når du har lært regnereglene blir utfordringen å omforme dagligdagse problemer til ligninger. Dette er et meget slagkraftig redskap, når du lærer å bruke det:
Eksempel 7:
Astrid er halvparten så gammel som Thorild. Knut er tre år eldre enn Thorild. Til sammen er de 53 år gamle. Hvor gammel er Astrid, Thorild og Knut?
Løsning:
Vi kaller alderen til Thorild for <math>x.</math>
Knut er: <math>x+3</math>
Når man legger sammen alderen til de tre, får følgende likning:
<math> \frac x2 + x + (x+3)=53</math>
<math> 2,5x =50</math>
<math> x =20</math>
Siden x er 20 betyr det at Thorild er 20 år, Astrid er 10 år og Knut 23 år gammel.
Operasjonenesrekkefølge
Dersom man har en ligning med både brøk og parentes kan den løses etter følgende oppskrift:
- multipliser ut parentesene
- sett parenteser rundt brøker med negative fortegn, dersom de har flere ledd i teller
- fjern brøkene ved å multiplisere alle ledd på begge sider av likhetstegnet med minste felles multiplum
- flytt og bytt slik at alle x ledd kommer på venstre side og alle ledd uten x på høyre side trekk sammen
- divider begge sider på koeffisienten foran x
To Ukjente
Innledning
Et likningssett er en samling (to eller flere) likninger i én eller flere variabler.
Ligningen 2x + 7 = 13 har en ukjent, x, og løses lett med metodene beskrevet i kapittelet om ligninger med en ukjent.
Vi kan ha flere ukjente, for eksempel to.
y = 2x + 1
Her er både x og y ukjente.
Ligningen har uendelig mange løsninger. Ligningen er et funksjonsutrykk for en rett linje.
Dersom ligninger med flere ukjente skal ha entydige løsninger må man ha like mange ligninger som man har ukjente.
Dersom vi har to ligninger med to ukjente, kalles dette et sett med ligninger, eller et ligningssett.
y = 2x + 1
y = - x + 4
Ligningene hører sammen. Målet er å finne en x- verdi og en y- verdi som passer i begge.
Source : Help with integrals integral calculator
Lineære likningssett
Lineære likningsett er likningssett som har variabler av første grad, som x og y. Vanlige løsningsmetoder er addisjonsmetoden, substitisjonsmetoden, og grafisk løsning.
Løsningsmetoder
Addisjonsmetoden
Addisjonsmetoden går som navnet tilsier ut på å legge sammen ligningene slik at vi får x eller y til å forsvinne. La oss legge sammen ligning (1) og (2). Vi ser at verken x eller y forsvinner sånn uten videre. Men, om vi først multipliserer ligning (2) med 2 ser vi at vi oppnår det vi ønsker. Vi får:
<math> y=2x+1 \\ \underline{y=-x+4 \quad | \cdot 2} \\ \quad \quad \quad y=2x+1 \\ \underline{ + \quad 2y=-2x+8} \\\quad \quad \quad 3y = 9 \\ \quad \quad \quad y=3</math>
Vi setter inn y = 3 i en av ligningene og får x = 1.
I beste fall kan vi addere ligningene direkte. Dersom den ukjente har en faktor med samme absoluttverdi, men med motsatt fortegn er det tilfelle.
Eksempel 8:
<math> -y = x - 5</math>
<math> y = x - 3</math>
Adder direkte og får
<math> 0 = 2x - 8</math>
<math> x=4</math>
Setter inn x = 4 i en av ligningene og får y = 4-3 =1
x = 4 og y = 1
I nest beste fall må man multiplisere en av ligningene slik at den ukjente forsvinner ved addisjon.
Eksempel 9:
<math> 2y = x + 4 </math>
<math> y =-x + 5</math>
Multipliser ligning to med minus to, før addisjon.
<math> 2y = x + 4</math>
<math> -2y = 2x - 10</math>
Legger sammen og får:
<math> 0=3x - 6</math>
<math> x = 2</math>
Setter man x = 2 gir det at y = 3
I verste fall må begge ligningene multipliseres med det som gir faktorenes minste multiplum.
Eksempel 10:
\begin{bmatrix}
3y = 6x - 3 \\
2y = -2x + 4
\end{bmatrix}
Dersom vi nå ønsker at y skal forsvinne må første likning multipliseres med 2 og den andre med -3 (kunne også brukt -2 og 3).
\begin{bmatrix} 6y = 12x - 6 \\ -6y = 6x -12 \end{bmatrix}
Legger så likningene sammen
0 = 18x - 18
x=1
Innsatt x = 1 gir y = 1
Innsettingsmetoden
Denne metoden går ut på å erstatte y i den ene ligningen med utrykket som inneholder x fra den andre likningen. y har samme verdi i begge ligningene, derfor kan vi gjøre dette (det samme gjelder for x).
Eksempel 11:
\begin{bmatrix}
y=2x+1 \\
2y = -x - 8
\end{bmatrix}
Vi setter uttrykket for y i første likning inn i andre og får en likning i x
\begin{bmatrix} y=2x+1 \\ 2(2x+1) = -x - 8 \end{bmatrix}
Regner så videre på den andre likningen.
4x+2=-x -8
5x = -10
x=-2
Setter inn x = - 2 i første likning og får y= -3.
Oppgaven er nå løst, men for å vise at det er likegyldig hvilken variabel man setter inn for løser vi samme oppgaven nedenfor ved å erstatte x. Svaret blir det samme.<math> y = 2x + 1 \quad \vee \quad 2y= -x -8 \\ y = 2x + 1 \quad \vee \quad x = -2y - 8 \\ y = 2(-2y - 8) +1 \\ y =-4y -16 +1 \\ 5y = -15 \\y=-3</math>
I andre linje er likning to ornet slik at x står alane på venstre side. Uttrykket er så satt inn i likning en, i tredje linje. Ved innsetting ser man at når y= -3 så blir x = -2, altså samme svar som over.Man bør bruke et par sekunder på å finne ut hvilen av variablene man ønsker å erstatte, ut fra hva som gir minst og lettest regning.
Eksempel 12:
<math> 2y = x + 1 </math>
<math> 3y = 7x - 4 </math>
Løser første ligning med hensyn på x:
<math> x = 2y - 1 </math>
<math> 3y = 7x - 4 </math>
Setter uttrykket for x inn i ligning to.
<math> 3y = 7(2y -1) -4 </math>
<math> 3y = 14y - 7 - 4 </math>
<math> -11y = -11 </math>
<math> y = 1 </math>
Innsatt i en av ligningene over gir det x = 1
x = 1 og y = 1
Grafisk løsning
Grafisk løsning vil si at den enkelte likning plottes i et koordinatsystem der y er en funkslon av x. Der grafene krysser hverandre finner man løsningen for x og y.
Eksempel 13:
Et likningsett er gitt ved: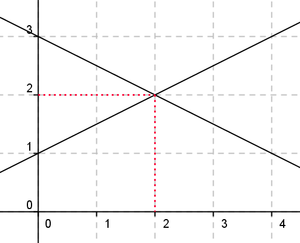
Eksempel 11:
<math> 3y-3 = 1,5x</math>
<math> y = -0,5x + 3</math>
Dersom man løser med blyant og papir, omformer du slik at du får y alene på venstre side. Du kan da tegne linjene ved hjelp av verditabell, eller ved hjelp av stigningstall og konstantledd.
<math> y = 0,5x +1</math>
<math> y = -0,5x + 3</math>
Plotter så grafene i et koordinatsystem og finner skjæringspunktet.
Ved inspeksjon ser man at likningssettet har løsning for
x = 2 og y = 2
Dersom man bruker Geogebra kan man taste inn likningene som dem står, uten å få y alene.
Dersom du får i oppgave å løse et ligningsett er det likegyldig hvilken metode du bruker, alle tre gir samme svar. Du bør allikevel beherske alle metodene da du ofte blir bedt om å løse ligningssettet ved hjelp av en spesiell metode.
Tre Ukjente
Man må alltid ha like mange uavhengige likningsett som man har ukjente. Tre ukjente krever tre likningen. Man kan bruke de samme metodene som når man har to ukjente.
Eksempel 14:
\begin{bmatrix}
x+y+z= 2 \\
2x + y + 2z = 1 \\
x-y-z =0
\end{bmatrix}
Dersom noe som dette dukker opp på del to er det lurest å bruke hjelpemidler for å spare tid.
Hver av likningen representerer et plan i det tredimensjonale rom. For hånd, med blyant og papir kan man gjøre slik:
\begin{bmatrix} x+y+z= 2 \\ 2x + y + 2z = 1 \\ x-y-z =0 \end{bmatrix} Løser første likning med hensyn på x.
\begin{bmatrix} x = 2-y - z \\ 2 (2-y - z) + y + 2z = 1 \\ (2-y - z)-y-z =0 \end{bmatrix} Setter inn uttrykket for x fra første likning inn i de to andre. Vi får da to likninger med to ukjente.
\begin{bmatrix} x = 2-y - z \\ 4-2y-2z + y + 2z = 1 \\ 2-2y-2z =0 \end{bmatrix} Regner ut og får: \begin{bmatrix} x = 2-y - z \\ 4-y =1 \\ 2-2y-2z =0 \end{bmatrix}
\begin{bmatrix} x = 2-y - z \\ y=3 \\ 2-2 \cdot 3-2z =0 \end{bmatrix}
\begin{bmatrix} x = 2-y - z \\ y=3 \\ z=-2 \end{bmatrix}
\begin{bmatrix}
x = 2-3 -(-2) = 1 \\
y=3 \\
z=-2
\end{bmatrix}
Altså samme resultat som ved bruk av CAS.
Tilbake til Ungdomstrinn Hovedside

