Løsning del 1 utrinn Vår 14

Oppgave 1

a) <math>831+1196=2027</math>

b) <math>987-789=198</math>

c) <math>14,2 \cdot 3,1 = 44,02</math>

d) <math>1620:120= \frac{1620}{120} = \frac{162}{12} = 13,5</math>

Oppgave 2

a) <math>3,25 \mathrm{h}=3 \cdot 60 \mathrm{min} + 0,25 \cdot 60 \mathrm{min} = 180 \mathrm{min} + 15 \mathrm{min} =195 \mathrm{min} </math>

b) <math>9,3 \mathrm{t} =9,3 \cdot 1000 \mathrm{kg}=9300 \mathrm{kg}</math>

c) <math> 2400 \mathrm{ cm^3 } = 2400 \mathrm{mL} = 2,4 \mathrm{L}</math>

d) <math> 36 \mathrm{km/h}= \frac{36}{3,6} \mathrm{m/s}=10 \mathrm{m/s}</math>

Oppgave 3

a) <math> 62000=6,2 \cdot 10^4 </math>

b) <math> ((-3)^2)^2-3^0=9^2-1=81-1=80</math>

Oppgave 4

a) <math> \frac{1}{5} + \frac{2}{5}= \frac{1+2}{5} = \frac{3}{5}</math>

b) <math> \frac{5}{2}- \frac{2}{3}= \frac{5 \cdot 3}{2 \cdot 3}- \frac{2 \cdot 2}{3 \cdot 2}= \frac{15}{6}- \frac{4}{6}= \frac{15-4}{6}= \frac{11}{6}</math>

c) <math> \frac{1}{4} \cdot \frac{2}{4}= \frac{1 \cdot 2}{4 \cdot 4}= \frac{2}{16} = \frac{1}{8}</math>

d) <math> 4: \frac{2}{3}= 4 \cdot \frac{3}{2}= \frac{12}{2}=6 </math>

Oppgave 5

a)

b)

Oppgave 6

Lønn for 1 times arbeid på kvelden: <math> 130 \mathrm{Kr} \cdot 1,25 = 162,50 \mathrm{Kr}</math>. Fire timers arbeid blir <math> 4 \cdot 162,5 \mathrm{Kr} = 650 \mathrm{Kr}</math>.

Alternativt kan man se på timene han jobber. 4 timer $\cdot$ 1,25 = 5, så han får lønn tilsvarende 5 arbeidstimer.

$5 \cdot 130 = 650$ kr.

Oppgave 7

a) <math> \frac{6a^3}{2a^2}= \frac{2 \cdot 3 \cdot a \cdot a \cdot a}{2 \cdot a \cdot a}=3a</math>

b) <math> \frac{6a-6}{12b^2}: \frac{a-1}{4b^3}= \frac{6(a-1)}{12b^2} \cdot \frac{4b^3}{a-1}= \frac{24 \cdot b \cdot b \cdot b}{12 \cdot b \cdot b} =2b</math>

Oppgave 8

a) Det er totalt fem kuler å trekke blant. Av disse er tre rød. Det gir sannsynligheten <math>P</math>(trekke rød kule)<math> = \frac{3}{5} = \frac{6}{10} = 60 \% </math>.

b) Første gang du trekker er sannsynligheten for å få en rød kule lik sannsynligheten <math>P</math> regnet ut i a). Andre gang du trekker, er det igjen 2 røde kuler og totalt 4 kuler. Det gir sannsynligheten <math>P</math> (trekke enda en rød kule) <math>= \frac{2}{4}= \frac{1}{2}</math>. Sannsynligheten for at begge disse to trekkene skjer etter hverandre, er lik produktet av dem; <math>P</math>(trekke 2 røde kuler uten tilbakelegging) <math>= \frac{3}{5} \cdot \frac{1}{2}= \frac{3}{10}= 30 \%</math>.

Oppgave 9

Setter prisen på ett skolebrød lik <math>S</math> og prisen på én vannflaske lik <math>V</math>. Fra oppgaven får vi to likninger:

(1): <math>85=2S+3V</math>

(2): <math>55=2S+V</math>

METODE 1: ADDISJONSMETODE (her vil denne være enklest):

Trekk likning (2) fra likning (1), (1)-(2):

<math>85-55=2S+3V-(2S+V)</math>.

Setter <math>V=15</math> inn i likning (2) (kunne godt valgt likning (1)) og finner <math>S</math>:

METODE 2: INNSETTINGSMETODE

Løser likning (2) for V (kunne godt valgt den andre likningen eller løst for S):

Erstatter <math>V</math> i likning (1):

Setter inn denne verdien for <math> S</math> i likning (2) og finner <math>V</math>:

Oppgave 10

<math> \frac{2 \mathrm{cm}}{100 \mathrm{km}}= \frac{0,02 \mathrm{m}}{100 \: 000 \mathrm{m}}= \frac{100 \cdot 0,02 }{100 \cdot 100 \:000 }= \frac{2}{10\:000\:000}= \frac{1}{5\:000\:000}</math>

Oppgave 11

Volumet som skal fylles med vann er 100 ganger så stort, så det vil ta 100 ganger så lang tid; <math>10 \mathrm{min} \cdot 100 = 1000 \mathrm{min} =\frac{1000}{60} \mathrm{h}=16 \mathrm{h}+40 \mathrm{min}</math>.

Oppgave 12

a) <math> S= \frac{3F+5}{2}= \frac{3 \cdot 25+5}{2}= \frac{80}{2}=40</math>

b) Vi skal finne <math>F</math>, og kan da sette <math>S=37</math> rett inn i den oppgitte formelen og regne ut. En noe penere løsning (først og fremst på del 2-oppgaver) er å først finne et generelt uttrykk for <math>F</math>:

<math>F= \frac{2S-5}{3}= \frac{2 \cdot 37-5}{3} \mathrm{cm}= \frac{74-5}{3} \mathrm{cm}= \frac{69}{3} \mathrm{cm}=23 \mathrm{cm}</math>

Oppgave 13

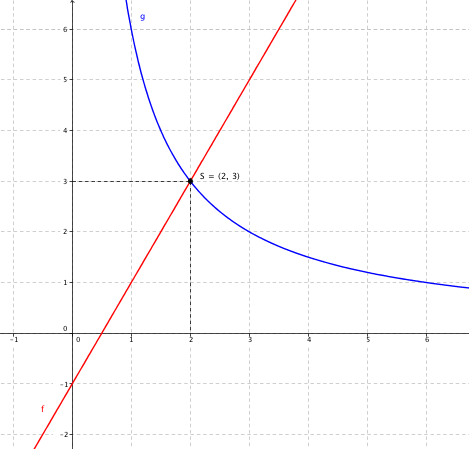
a)

x	f(x)	Koordinater (x,y)
0	-1	(0,-1)
1	1	(1,1)
2	3	(2,3)
3	5	(3,5)

x	g(x)	Koordinater (x,y)
1	6	(1,6)
2	3	(2,3)
3	2	(3,2)
4	1,5	(4, 1,5)
5	1,2	(5, 1,2)

b)

c) Leser av grafen over og ser at skjæringspunktet er <math>S(2,3)</math>. Kan også regne oss fram til skjæringspunktet ved å sette <math>f=g</math>, men da får vi en annegradslikning (der vi må bruke ABC-formelen) som ikke er pensum for ungdomsskolen. En konsekvens av at vi får en annengradsfunksjon er at vi får to skjæringspunkter. Det andre skjæringspunktet har koordinater <math>S(-1.5, -4)</math>, og er dermed ikke synlig i koordinatsystemet over.

Oppgave 14

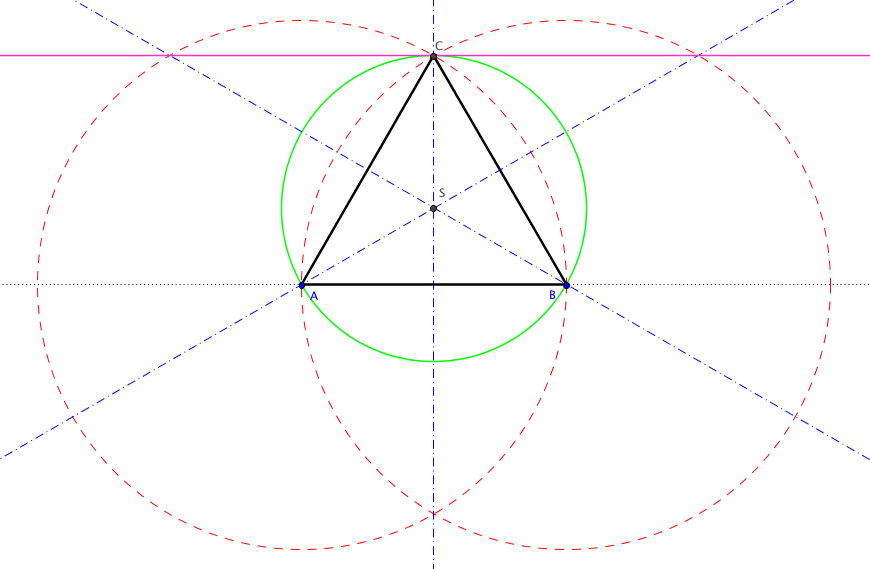
Avsett et linjestykke AB=7 cm. Lag en sirkel (rød på figuren under) med sentrum i A og radius 7 cm. Lag en tilsvarende sirkel i B (med samme radius, også rød på figuren). Skjæringspunktet mellom sirklene er punktet C. Trekk linjene AC og BC.

Konstruer midtnormalene på sidene i trekanten (blå på figuren under). Slå en sirkel (grønn på figuren under) om skjæringspunktet S med radius lik avstanden fra S til et av hjørnene. Sirkelen skjærer da gjennom alle hjørnene.

For å konstruere en tangent (rosa på figuren under) til sirkelen i C, konstruerer du en 90 graders vinkel i C på midtnormalen til AB.

Jeg har konstruert i Geogebra, men du må gjøre med passer for hånd.

PS: Der det i oppgaveteksten står "En sirkel går gjennom punktene i <math> \Delta ABC</math>", må de mene at sirkelen skjærer gjennom alle hjørnene til trekanten.

Oppgave 15

a) Pytagoras gir;

<math>(AB)^2=(6 \mathrm{m})^2+(8 \mathrm{m})^2</math>

<math>AB= \sqrt{36 \mathrm{m^2}+64 \mathrm{m^2} }= \sqrt{100 \mathrm{m^2}} =10 \mathrm{m}</math>

b) Ettersom <math>BD</math> er 4 ganger så lang som <math>CE</math>, er <math>AD</math> 4 gnager så lang som <math>BE</math>. Vi får

<math>BE= \frac{AD}{4}= \frac{6 \mathrm{m}}{4}=1,5 \mathrm{m}</math>

Oppgave 16

METODE 1:

Arealet <math>T</math> er gitt ved sidelengde gange sidelengde:

METODE 2:

Arealet <math>T</math> av det store kvadratet er også lik summen av de fire mindre firkantene: