Løsning del 1 utrinn Vår 13
DEL 1
Ingen hjelpemiddler
Oppgave 1
a) 1292 + 576 = 1868
b) 954 - 428 = 526
c) <math>4,3 \cdot 7,5 = 32,25</math>
d) 1206 : 3 = 402
Oppgave 2
a) 218 min = 3 timer og 38 minutter.
b) 8hg = 0,8 kg
c) 4500mm = 4,5m
d) <math>50 dm^2 = 0,5m^2 </math>
Oppgave 3
a) <math>(4-2)^2 +2^3 = 2^2 + 8 = 4+8 = 12</math>
b) <math> \frac{-2^2 \cdot (-2) \cdot 2^0}{2^2} = \frac{-4 \cdot (-2) \cdot 1}{4} = \frac 84 = 2</math>
Oppgave 4
a) <math>\frac 14 + \frac 24 = \frac 34</math>
b) <math>\frac 23 - \frac 12 = \frac 46 - \frac 36 = \frac 16</math>
c) <math>\frac 23 \cdot 12 = \frac {2 \cdot 12}{3} = \frac{24}{3} = 8</math>
d) <math>\frac 43 : \frac 23 = \frac 43 \cdot \frac 32 = \frac {4 \cdot 3}{3 \cdot 2 }= 2</math>
Oppgave 5
a)
<math> 4x-1 =3x \\4x-3x = 1 \\ x=1</math>
b)
<math>\frac 45(x-1) = 1 + \frac x2 \quad | \cdot 10\\ 8(x-1) = 10+5x \\ 8x-8 = 10+5x \\ 8x-5x = 10+8 \\ 3x=18 \\ x = 6</math>
Oppgave 6
Overslag.
<math>15 kr \cdot 6 + 50kr/kg \cdot 2kg = 90kr +100kr = 190kr </math>
Man må betale i underkant av 190 kr.
Oppgave 7
Når noe er redusert med 25 % kan vi multiplisere med 0,75.
<math> x \cdot 0,75 = 3000kr \\ x = \frac{3000kr}{0,75} = 4000 kr</math>
Oppgave 8
a)
1 + 3 + 4 + 4 + 4 + 5 + 5 + 5 + 6 + 6 = 43
b)
43 : 10 = 4,3
Oppgave 9
a)
a-(a-2a) = a - a + 2a = 2a
b)
<math>\frac{x^2y^2 + xy^2}{xy^2} = \frac {xy^2(x+1)}{xy^2} = x+1</math>
Oppgave 10
Sannsynlighet for en sekser: <math>\frac 16</math>
Sannsynlighet for to like når man kaster to terninger: Det er seks ganger seks mulige utfall. For to like er det seks utfall. Gunstige på mulige blir da seks trettiseksdeler, som er en sjettedel. Altså er sannsynligheten for begge hendelsene like store.
Oppgave 11
x = antall epler
y = antall bananer
5x + 6y = 80
x = 2y
setter inn for x i første likning og får:
5(2y) + 6y = 80
16y = 80
y = 5
dvs
x= 10
Sondre kjøper 10 epler og 5 bananer.
Oppgave 12
25 km = 25 000m = 2 500 000cm
<Math> \frac{1}{1\: 000\: 000} = \frac{x}{2\: 500\: 000} \\ x= 2,5</Math>
Avstanden mellom de to stedene er 2,5 cm på kartet.
Oppgave 13
<Math>60km/t \cdot 2,5t = 150km</Math>
På to og en halv time kjører en bil 150 km, dersom den holder en fart på 60 kilometer i timen.
Oppgave 14
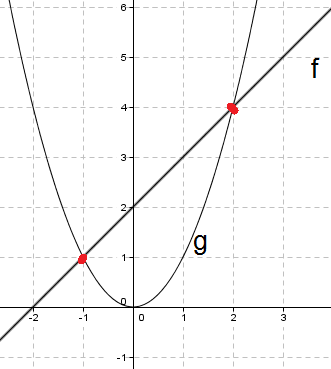
a)
| x | f(x) | Koordinater (x,y) |
|---|---|---|
| -2 | 0 | (-2,0) |
| -1 | 1 | (-1,1) |
| 0 | 2 | (0,2) |
| 1 | 3 | (1,3) |
| 2 | 4 | (2,4) |
| x | g(x) | Koordinater (x,y) |
|---|---|---|
| -2 | 4 | (-2,4) |
| -1 | 1 | (-1,1) |
| 0 | 0 | (0,0) |
| 1 | 1 | (1,1) |
| 2 | 4 | (2,4) |
b)
c)
Skjæringspunktene mellom f og g er (-1,1) og (2,4).
Oppgave 15
Jeg har brukt Geogebra til konstruksjonen. Du må bruke blyant, linjal og passer, siden dette er del en.
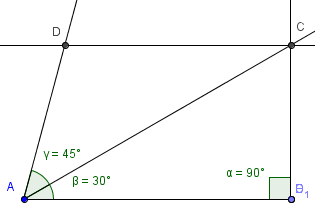
Forklaring:
Avsetter linjestykke AB lik 8 cm. I punkt B konstrueres 90 grader. I punkt A konstrueres 30 grader, ved å halvere en 60 graders vinkel. Linjestrålene fra A og B forlenges og skjærer hverandre i punkt C. I A konstruerer man 90 grader på AC. Denne vinkelen halverers til 45 grader og linjestrålen forlenges oppover. Til slutt konstruerer man en linje gjennom C, parallell med AB. Der denne linjen skjærer linjestrålen som danner 45 grader med AC ligger D.
Oppgave 16
a)
Areal:
Rektangel:<Math>20m \cdot 50m = 1000m^2</Math>
Trekant: <Math>\frac{30m \cdot 40m}{2} = 600m^2 \\ \text {Sum : }1600m^2 </Math>
Volum; <Math> 1600m^2 \cdot 0,1m = 160m^3</Math>
Det trengs 160 kubikkmeter grus for å dekke området med ti centimeter grus.
b)
Den eneste delen av omkretsen som er ukjent er hypotenusen i trekantdelen. Denne er: <Math>hyp^2 = (30m)^2 + (40m)^2 \\ hyp^2 = 900m^2+1600m^2 \\ hyp = 50m</Math>
Da blir omkretsen av området, og lengden av gjerdet : 50m + 50m + 10m + 20m + 50m = 180m
Oppgave 17
<Math>V_{kule} = \frac 43 \pi r^3, \quad V_{sylinder} = \pi r^2 h \\ 3 \cdot V_{kule} =V_{sylinder} \\ 4 \pi r^3 = \pi r^2 h \\ \Downarrow \\ h = 4r </Math>