Løsning del 1 utrinn Vår 12

Oppgave 1

a) 334+465 = 799

b) 854 - 328 = 526

c) <math>4,3 \cdot 74 = 318,2 </math>

d) 664 : 40 = 16,6

Oppgave 2

a) 1500 ml = 1,5 l

b) 4,7 tonn = 4700 kg

c) 4500 mm = 45 dm

d) <math> 25\:000 m^2 = 25 \text{ dekar (mål)} </math>

Oppgave 3

a) <math>3 + 3(3-2)^2 = \\ 3+3 \cdot 1^2 = \\ 3+3 = 6</math>

b) <math>-3^2(-3+2)^2 = \\ -9(-1)^2 = -9</math>

Oppgave 4

a) <math> \frac 38 + \frac 18 = \frac {3+1}8 = \frac 48 = \frac 12 </math>

b) <math> \frac 23 - \frac 16 = \frac 46 - \frac 16 = \frac {4-1}6 = \frac 12 </math>

c) <math> \frac 24 \cdot \frac 36 = \frac {2 \cdot 3}{4 \cdot 6}= \frac 14 </math>

d) <math> 3 : \frac 35 = 3 \cdot \frac 53 = 5 </math>

Oppgave 5

a) <math> 9x-13 = 6x +2 \\ 9x -6x = 2 + 13 \\ 3x = 15 \\ x=5</math>

b) <math>2(x-1) = 1 + \frac x2 \quad | \cdot 2\\ 4(x-1) = 2 + x \\ 4x-4 = 2+x \\ 3x = 6 \\ x= 2</math>

Oppgave 6

<math> \frac 1x = \frac{3cm}{3km} \\ \frac 1x = \frac{3cm}{300\:000cm}\\ 3x = 300\:000 \\ x = 100\:000</math>

Målestokken er 1: 100 000

Oppgave 7

Dersom man får 50% rabatt betaler man halvparten av ordinær pris. Dersom man får 40% rabatt betaler man "litt" mere enn halv pris. Ut fra alternativene ser man at jakken derfor må ha kostet ca. 800kr. før rabatten. Dersom man deler 475kr på 0,6 (4750 : 6) får man i underkant av 800 kroner.

Med utregning ville man skrevet det slik:

$x \cdot 0,6 = 475 \\ x = \frac{475}{0,6} \\ x \approx 800$

Oppgave 8

<math>\frac{140}{400} = \frac{x}{600} \\ 400x = 600 \cdot 140 \\ x = 210 </math>

Biggie koster kr. 210,-

<math>\frac{140}{400} = \frac{x}{100} \\ 400x = 100 \cdot 140 \\ x = 35 </math>

Mini koster kr. 35,-

Alternativ løsning:

Vi ser at "Mini" er en fjerdedel av "Normal", den vil derfor koste en fjerdedel av prisen. $\frac{140}{4} = 35$ kr.

"Biggie" er seks ganger større enn "Mini", altså $ 35 \cdot 6 = 210 $ kr.

Oppgave 9

a) <math> 4a-(a+2a) = \\ 4a - 3a = a</math>

b)<math>\frac{x^2y+xy^2}{xy} = \frac{xy(x+y)}{xy} = x+y</math>

Oppgave 10

a) En gunnstig av fem mulige:

<math>\frac15 = 20 \%</math>

b) Han kan først trekke Soland Gunnersen og så Ludvig, eller han kan trekke Ludvig og så Soland Gundersen.

<math>2 \cdot \frac 15 \cdot \frac 14 = \frac 1{10}</math>

Oppgave 11

<math>C= \frac{ F-32}{1,8 } \\ 1,8C = F-32 \\ F = 1,8C + 32</math>

Oppgave 12

Pris flaske = x

Pris eple = y

<math> 1)\: 2x+2y=40 \\2)\: x+3y= 32 \\ 2) \: x = 32-3y \\ \text{Setter likning 2 inn i likning 1}\\ 2(32-3y) + 2y=40 \\ 64-6y+2y =40 \\ -4y = -24 \\ y=6 \\ \text{som gir x = 14}</math>

Vannet koster 14 per flaske, og et eple koster 6 kroner.

Oppgave 13

a) Medianen er tallet i midten når observasjonene står i stigene rekkefølge

169, 170, 170, 173, 174, 175, 178

Det midterste tallet, altså medianen er 173 cm.

b) <math> \frac{170+169+170+175 }{4 }cm =171cm</math>

Oppgave 14

<math> 5^2+12^2 = 25 + 144 = 169\\ 13^2 = 169</math>

Konklusjonen er at (5, 12, 13) er et pytagoreisk talltrippel.

Oppgave 15

Overslag:

Planken koster 9,95 kr per meter <math> \approx </math> 10 kr. per meter.

<math> 487 cm \approx 5m \\ 353cm \approx 3,5m \\ 506 cm \approx 5m \\ 309 cm \approx 3m \\ 422cm \approx 4m \\ \\ (5+3,5 + 5 + 3 +4 )m \cdot 10kr/m \approx 200kr</math>

Oppgave 16

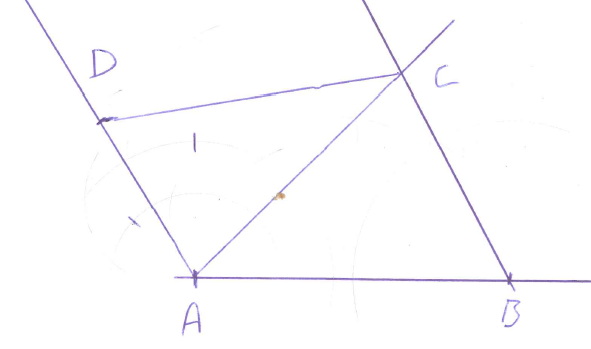
Trekk linjestykket AB, 7cm.

Sett passerspissen i B og konstruer 60 grader, trekk linjen.

Sett passerspissen i A og konstruer 90 grader. Halver vinkelen og den blir 45 grader. Trekk linjen opp mot linjen fra B. Der linjene krysser hverandre ligger punkt C.

Sett passerspissen i A og konstruer 75 grader på AC. Konstruer 60 + 60 og halver den ene 60 graderen to ganger, det gir 75 grader. Trekk linjen og mål 4 cm. og avsett punktet D.

Trekk linjen CD.

Oppgave 17

<math> y= -x^2+2 \quad \quad B\\ y=2x+2 \quad \quad A \\ y= \frac 2x \quad \quad D \\ y= -2x+2 \quad \quad C</math>

Oppgave 18

a)

Areal av trekant ABC:

<math>A = \frac{gh}{2} = \frac{4cm \cdot 3cm}{2} = 6 cm^2</math>

b)

Volumet av prisme:

<math>V = Gh = 6cm^2 \cdot 3,5 cm = 21 cm^3</math>

c)

Overflate av prisme:

Eneste siden vi mangler for å regne ut overflaten er hypotenusen i trekanten, den finner vi ved Pytagoras.

$BC = \sqrt{4^2 + 3^2} = 5$

<math> 6cm^2 + 6cm^2 + 3cm \cdot 3,5cm + 4 cm \cdot 3,5cm + 5cm \cdot 3,5 cm = 54cm^2</math>

Oppgave 19

Dersom vinkel B er 60 grader har man en 30,60, 90 graders trekant. Da er hypotenusen dobbelt så lang som det korteste katetet, altså 8,0m.

<math>(7m)^2 +(4m)^2 = 65m^2 \\ \sqrt{65m^2} > 8m</math>

Vinkel B er ikke 60 grader.