Koordinatsystemet
Koordinatsystem
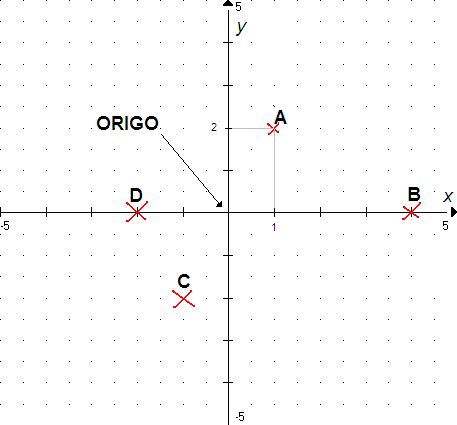
Et koordinatsystem består av to tallinjer som står vinkelrett på hverandre. Vi kaller disse tallinjene for akser. Punktet der aksene krysser hverandre kalles for origo. Den vannrette aksen kalles for x- aksen eller første aksen. Den loddrette aksen kalles for y- aksen eller andre aksen.
Et punkt kan bestemmes med to tall ( et tallpar ) som vi kaller koordinater. Tallpar skrives på formen (x,y). Origo har koordinatene (0, 0). Man oppgir alltid x verdien først . Punktet (1,3) har verdiene x = 1 og y = 3. Her er eksempler på noen punkter: A (1,2), B (4,0), C (-1, -2), D (-2, 0).
Graf
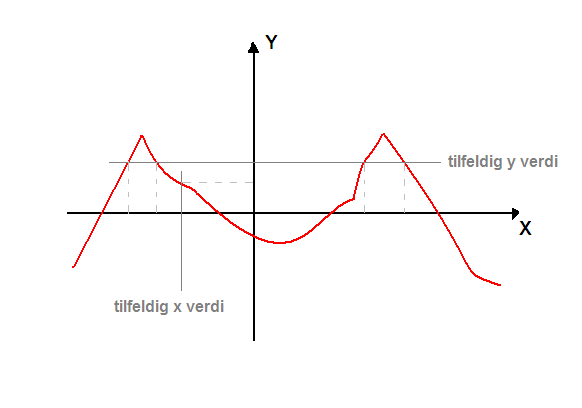
En graf er en kurve (linje) som viser sammenhengen mellom to variable størrelser, for eksempel x og y.
Det er viktig å legge merke til at dersom kurven representerer en funksjon finnes det bare en Y verdi for hver X verdi. For en Y verdi kan det finnes flere X verdier. Dersom x er forskjellige tidspunkt på dagen og y er temperaturen, betyr det at et tidspunkt kan kun ha en temperatur, men en temperatur kan ha forekommet flere tider på dagen.
Funksjon
Hva er en funksjon?
La oss tenke oss en liten tunnel som det går an å kjøre en bil gjennom. Hver gang en rød bil kjører inn i tunnelen er den blå når den kommer ut. Når en svart bil kjører inn er den blå når den kommer ut. Når en grønn bil kjører inn er den blå når den kommer ut. Når en blå bil kjører inn er den blå når den kommer ut.
Hva er tunnelens funksjon?
Jo, den maler alle biler blå.
La oss tenke oss at vi har en liten boks med et hull i toppen og et i bunnen. Når vi putter et tall inn i toppen kommer et annet tall ut i bunnen. La oss gi boksen vårt et navn. La oss kalle den for Y.
Vi putter tallet 3 inn og får ut tallet 5.
Vi putter tallet 1 inn og får ut tallet 3.
Vi putter tallet 7 inn og får ut tallet 9.
Vi putter tallet -3 inn og får ut tallet -1.
Vi putter tallet -1 inn og får ut tallet 1
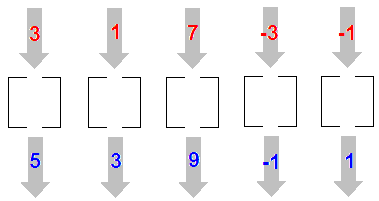
Hva gjør boksen? Den legger til to til det tallet som blir stappet inn i boksen. Vi kallet boksen for Y? La oss kalle tallet vi putter inn for x.
Vi kan skrive dette slik matematisk:
(1) Y = X + 2
Y = X + 2 kalles for funksjonsutrykket. Vi sier at Y er en funksjon av X. Verdien av Y avhenger av verdien av X. Detter er det vi kaller en lineær funksjon, dvs. en rett linje.
Den Rette Linje
Det at en funksjon er lineær betyr at om vi tegner grafen i et koordinat system med X verdier på førsteaksen og Y verdier på andreaksen får vi en rett linje.
Alle lineære funksjoner er av typen (2) Y = aX + b
I vårt eksempel er a = 1 og b = 2.
Vi må se litt nærmere på hvordan vi tegnet grafen.
Verditabell
Måten vi tegner grafen til en funksjon på er at vi lager en verditabell, det vil si en tabell som har X og Y verdier.
Vi velger selv X verdier. Når vi har valgt en X verdi setter vi den inn for X i funksjonstrykket (1). Da får vi en Y verdi som hører til X verdien.
Disse resultatene setter vi inn i en tabell, som vist nedenfor. Ut i fra disse verdiene tegner vi grafen. I vårt eksempel kan verditabellen se slik ut:
x -1 0 1 2 y 1 2 3 4
Og grafen ser slik ut:
Når funksjonen er lineær, dvs. er en rett linje, trenger vi kun to punkter for å kunne tegne grafen. (I Funksjoner II skal vi se at ikke alle funksjoner er lineære. I slike tilfeller trenger vi flere punkter.)
La oss se litt nærmere på ligningen Y = aX + b
Det tallet som står foran X forteller hvordan linjen stiger.
Dersom a er positiv betyr det at grafen stiger mot høyre, med økende x verdi. Desto høyere a verdi, desto brattere stiger grafen.
Dersom a er negativ betyr det at Y avtar mot høyre, eller med økende X verdi.
Tallet b forteller hvor grafen krysser Y aksen. Når grafen krysser Y aksen er X verdien lik null.
Vi ser at om vi setter X lik null inn i funksjonsutrykket får vi Y = b.
Når du får litt trening kan du tegne grafen til en rett linje direkte fra funksjonsutrykket, bare ved å se på a og b, men husk at en verditabell vil alltid kunne være til hjelp.
Ettpunktsformelen
Dersom du kjenner et punkt på linjen og stigningstallet kan du finne funksjonsutrykket ved å bruke følgende formel:
Ligningen for en rett linje gjennom et punkt (x1,y1) med stigningstall a.
Ved å se på figuren over kan vi vise at ligning (3) stemmer. Stigningstallet a er endring i Y verdi delt på endring i X verdi, når man beveger seg bortover grafen:
Topunktsformelen
Dersom man kjenner to punkter på en rett linje er stigningstallet a gitt som:
Om vi kombinerer ligning(6) med ligning(3) får man formelen for en rett linje, basert på at man kjenner to punkt på linjen,
topunktsformelen: