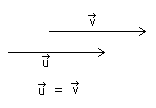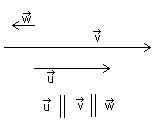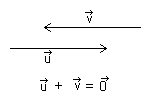Introduksjon til vektorer
En vektor er en tallstørrelse med retning. Fart, akselerasjon og kraft er eksempler på vektorer. En skalar størrelse er ikke en vektor fordi en skalar størrelse ikke har en retning.
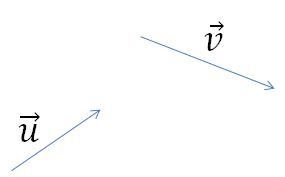
Vi tegner vektoren som en pil, der pilens lengde indikerer størrelse og pilens orientering gir retningen.
Vektorer navnsettes gjerne med en eller to bokstaver med en pil pekende mot høyre, over seg. Man ser at u og v er to forskjellige vektorer, de har både forskjellig lengde og forskjellig rettning.
Like vektorer
1.To vektorer er like dersom vektorene har samme retning og samme lengde.
Parallelle vektorer
2.To vektorer er parallelle dersom vektorene har samme retning eller motsatt retning.
Addisjon og subtraksjon av vektorer
Sum av vektorer
Det er to alternative måter å tenke på ved addisjon av vektorer.
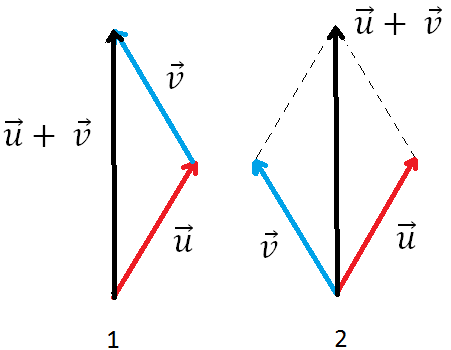
Figur 1: Dersom man vil summere u og v vektor kan man parallforskyve den ene, slik at den starter der den andre slutter ( v begynner der u slutter). Hvilken man kopler i "halen" på den andre er likegyldig.
Vektorsummen u + v blir en ny vektor som begynner der den første vektoren begynner, og slutter der den siste slutter. Man kan summere så mange vektorer man ønsker på denne måten.
Figur 2: Alternativt kan man la begge vektorene starte i samme punkt. De vil utspenne et parallellogram. Diagonalen i parallellogrammet utspennt av u og v vil være vektorsummen u + v.
Differansen mellom vektorer
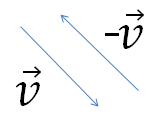
To vektorer som er like lange, parallelle og motsatt rettede er motsatte vektorer.
<math> \vec v = - \vec v </math>
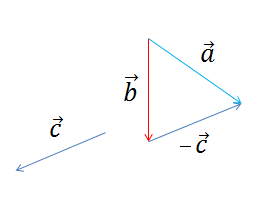
Differansen mellom to vektorer kan sees som summen av flere vektorer der en eller flere av vektorene er negative.
<math> \vec a = \vec b + (- \vec c) </math>
Nullvektor
4.Nullvektor har lengde null og er parallell med alle andre vektorer.
5.Lengen av n vektor skrives som
<math>| \vec n |</math>
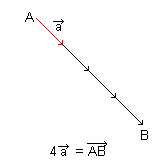
6.En vektor multiplisert med en skalar størrelse beholder retningen til den opprinnelige vektoren, men lengen øker med en faktor tilsvarende den skalare størrelsen.
Vektorlikninger
Det forutsettes at vektorene u og v ikke er parallelle:
<math>3\vec u +m\vec v = - \vec v + n\vec u \\ n=3 \wedge m=-1 </math>