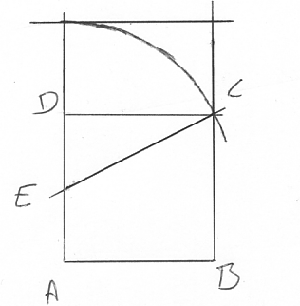
Høydeling ved konstruksjon
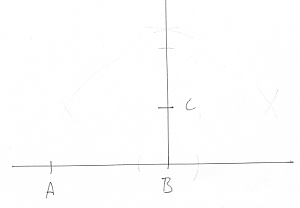
Det gylne snitt eller høydeling kan konstrueres som følger:
•Avsett linjestykket AB
•Konstruer normalen til AB gjennom B (eller A)
•Avsett C slik at BC = 0,5AB
•Trekk linjen AC
•Sett passerspissen i C og slå en sirkelbue med radius BC, slik at den skjærer AC i D. •Sett passerspissen i A og slå en sirkelbue med radius AD, slik at den skjærer AB i E.
Linjestykket AB er høydelt i E.
Gyllen trekant
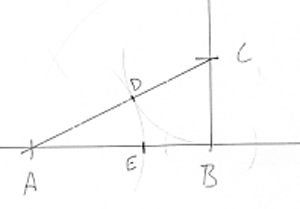
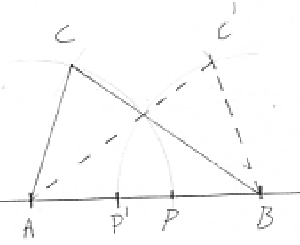
Høydel et linjestykke som vist over. En høydelt (gyllen) trekant konstrueres på følgende måte:
•Høydel et linjestykke som vist over (P eller/og P').
•Sett passerspissen i A og slå en sirkelbue med radius AP (eventuelt AP' fra B).
•Sett passerspissen i B og slå en sirkelbue med radius AB (eventuelt det samme fra A).
En gyllen trekant er likebeint og har vinkler som er 72°, 72° og 36°. Vi legger merke til at 36° er 1/10 av gradeantallet i en sirkel.
Regulær tikant
Konstrueres ved å benytte det vi vet om gylne trekanter. Tegn en sirkel og høydel radien. Konstruer en gyllen trekant slik at vinkelen på 36° ligger i sirkelens sentrum. Når du har konstruert trekanten som beskrevet over har du to punkter på sirkelperiferien. Buen mellom punktene utgjør 1/10 av sirkelens omkrets. Bruk passer og avsett den samme lengden rundt hele sirkelperiferien. Du har nå ti punkter på sirkelperiferien og trekker linjene mellom disse. Den regulære tikanten er nå ferdig.
Regulær femkant
Samme som over, men du hopper over annethvert punkt på sirkelperiferien.
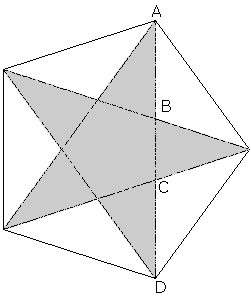
Pentagram
Pentagrammet har en stjerneform med fem armer, derav penta. Figuren konstrueres lett ved å ta utgangspunkt i tikanten over. Det som er spesielt med figuren er alle høydelingene. AD er høydelt i B og C, AC er høydelt i B og BD er høydelt i C, osv.
Gyllent rektangel
Et gyllent rektangel har langsider og kortsider hvis forhold utgjør det gylne snitt.
Dersom du kjenner langsiden av rektangelet gjøres konstruksjonen ved å høydele denne, Lengden av kortsiden er da gitt og rektangelet konstrueres direkte.
Dersom man kjenner lengden av kortsiden går man veien om konstruksjon av et kvadrat.
• Konstruer kvadratet ABCD der lengden av sidene er lik kortsidene i rektangelet.
• Halver en av sidene (AD) og trekk linjen fra en av de to motstående hjørner (C) til E.
• Til AE legges lenden av EC. Dette er lengden av langsiden, som gir høydeling.