Den rette linje
Lineære funksjoner
Det at en funksjon er lineær betyr at om vi tegner grafen i et koordinat system med X verdier på førsteaksen og Y verdier på andreaksen får vi en rett linje. Det generelle funksjonsuttrykket er:
<math> Y = aX + b </math>
a kalles for stigningstallet og b for konstantleddet. Dersom x er null er Y lik b. Konstantleddet b forteller hvor grafen krysser y-aksen. a forteller hvor mange enheter man beveger seg i y rettning (opp eller ned), når man beveger seg en enhet til høyre på x aksen.
Dersom a er positiv betyr det at grafen stiger mot høyre, med økende x verdi. Desto høyere a verdi, desto brattere stiger grafen.
Dersom a er negativ betyr det at Y avtar mot høyre, eller med økende X verdi.
Tallet b forteller hvor grafen krysser Y aksen. Når grafen krysser Y aksen er X verdien lik null.
EKSEMPEL:
Vi har funksjonsuttrykket: <math> Y = \frac12X + 2 </math>
Grafen ser slik ut:
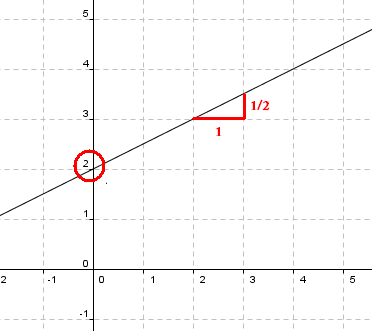
Man observerer at grafen går gjennom punktet (0,2) på y aksen. Stigningstallet er <math>\frac12</math>. Det betyr at når man beveger seg en enhet til høyre må man bevege seg 0,5 (en halv) oppover i y rettning for å treffe grafen igjen.
Dersom man har kontroll på stigningstall og konstantledd er det greit å tegne grafen med bare disse to størrelsene. Dersom man synes dette er vannskelig er det lurt å lage en verditabell.
Verditabell
Vi velger selv tilfeldige X verdier. Det er gjerne lurt å velge verdier som ligger nærheten av origo.
Når vi har valgt en X verdi setter vi den inn for X i funksjonstrykket (1). Da får vi en Y verdi som hører til X verdien.
Disse resultatene setter vi inn i en tabell. Ut i fra disse verdiene tegner vi grafen. I vårt eksempel kan verditabellen se slik ut:
Verditabell er en samling av punkter på grafen, altså sammhørende verdier av x og f(x). Formålet med å lage en verditabell er at du har nok punkter til å kunne tegn eller skissere grafen.
Det anbefales at du lærer deg å bruke kalkulatoren når du skal lage verditabeller.
Av og til er det imidlertid nødvendig å kunne lage tabellen manuelt. Det gjøres ved at du selv velger et antall x verdier i det området du skal tegne grafen. Du setter inn x verdiene i funksjonsuttrykket og finner sammhørende funksjonsverdier. Hvor mange verdier du velger kommer an på hvor nøyaktig du ønsker det. Flere verdier gir økt nøyaktighet.
Eksempel:
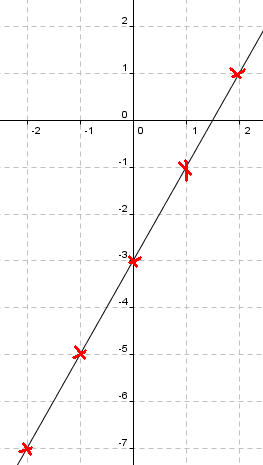
Vi ønsker å tegne grafen til f(x) = 2x -3 i området fra x = -2 til x = 2.
Vi velger x lik -2, -1, 0, 1, 2 og får:
x f(x)= 2x - 3 f(x) (x, f(x)) -2 f(-2) = 2 (-2) - 3 f(-2)= -7 (-2, -7) -1 f(-1) = 2 (-1) – 3 f(-1) = -5 (-1,-5) 0 f(0) = 2 (0) – 3 f(0)= -3 (0, -3) 1 f(1) = 2 (1)– 3 f(1)= - 1 (1, -1) 2 f(2) = 2 (2) – 3 f(2) = 1 (2, 1)
Og grafen ser slik ut:
Ettpunktsformelen
Dersom du kjenner et punkt på linjen og stigningstallet kan du finne funksjonsutrykket ved å bruke følgende formel:
<math> y-y_1 = a(x-x_1) </math>
a er stigningstallet og <math>(x_1 , y_1) </math> er koordinatene til punktet.
Hva er funksjonsuttrykket til en funksjon som har stigningstall 2 og går gjennom punktet (-2,
-1)?
<math> y-(-1) = 2(x-(-2)) </math>
<math> y = 2x + 3 </math>
Topunktsformelen
Dersom man kjenner to punkter på en rett linje er stigningstallet a gitt som:
<math> a =\frac{\Delta y}{\Delta x}=\frac{y_2 - y_1}{x_2 - x_1} </math>
Desom man setter dette uttrykket inn i etpunktsformelen over får man:
<math> y- y_1=\frac{y_2 - y_1}{x_2 - x_1}(x-x_1) </math>
<math> EKSEMPEL </math>