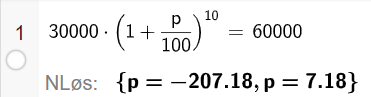2P 2022 vår K06 LØSNING
Diskusjon av denne oppgaven på matteprat
DEL 1
Oppgave 1
a)
Skriver tallene i stigende rekkefølge:
2 2 4 4 5 5 5 6 6 10
Medianen gjennomsnittet av de to midterste tallene, som begge er 5. Medianen er altså $5$.
Gjennomsnitt: $\frac{2+2+4+4+5+5+5+6+6+10}{10}=\frac{49}{10}=4,9$
Typetallet er det tallet som forekommer flest ganger, nemlig $5$.
Variasjonsbredden er differansen mellom det høyeste og det laveste tallet: $10-2 = 8$
b)
For å finne relativ frekvens for fem fjellturer, tar vi antall forekomster av 5 fjellturer, og deler på antall år med fjellturer:
$\frac{3}{10}=0,3$.
Det forteller oss at 30% av årene, har Sebastian gått 5 fjellturer.
For å finne kumulativ frekvens, legger vi sammen antall forekomster av 5 eller færre fjellturer i året:
$2+2+3 = 7$
Det forteller oss at 7 av årene, har Sebastian gått 5 eller færre fjellturer i året.
Oppgave 2
$\frac{5\cdot 10^6+1,5\cdot 10^7}{2,5\cdot 10^{-6}}$
$ = \frac{5\cdot 10^6+15\cdot 10^6}{2,5\cdot 10^{-6}}$
$ = \frac{20\cdot 10^6}{2,5\cdot 10^{-6}}$
$ = 8\cdot 10^{6-(-6)}$
$ = 8\cdot 10^{12}$
Oppgave 3
a)
Finner 5 % av 600 000 kr:
10 % av 600 000 kr er 60 000 kr. 5 % av 600 000 kr er derfor 30 000 kr.
Verdien av båten om ett år vil være:
600 000 kr - 30 000 kr = 570 000 kr.
b)
Eirik tror at båtens verdi synker lineært med 30 000 kr per år. Til sammen 30 000 kr * 5 = 150 000 kr, som ville gi båten en pris på 450 000 kr om 5 år.
Det kan ikke stemme at båtens verdi synker like mye hvert år, fordi båtens verdi synker eksponentielt (det er en prosentvis nedgang). Det første året synker båtens verdi med 5 % av 600 000 kr, som er 30 000 kr. Det andre året er båten verdt 570 000 kr, og båtens verdi vi synke med 5 % av 570 000 kr, som er mindre enn 30 000 kr. Båtens verdi synker altså med et mindre beløp for verdt år.
Oppgave 4
a)
$K(x)=ax+b$
Vi har punktene (8,54) og (16,58) på grafen.
Finner stigningstallet a: $\frac{58-54}{16-8}=\frac{4}{8}=\frac{1}{2}$
Stigningstallet forteller oss at kartlaven vokser med en halv mm i diameter per år. Jeg antar at det er snakk om ett individ av kartlav.
Finner konstantleddet b: $54-\frac{1}{2}\cdot 8 = 54 - 4 = 50$
Konstantleddet forteller oss at den observerte kartlaven hadde en diameter på 50 mm ved første observasjon.
b)
I løpet av 200 år øker diameteren med kartlaven med $\frac{1}{2} mm/ år \cdot 200\, år = 100 \, mm$, det vil si $10\, cm$.
Oppgave 5
a)
| Antall krabber | Klassemidtpunkt (m) | Antall dager (f) | m*f |
|---|---|---|---|
| [0,20> | 10 | 5 | 50 |
| [20,30> | 25 | 10 | 250 |
| [30,40> | 35 | 10 | 350 |
| [40,60> | 50 | 15 | 750 |
| [60,100> | 80 | 20 | 1600 |
| Sum | 60 | 3000 |
Gjennomsnitt: $\frac{3000}{60} = 50$
Det var i gjennomsnitt 50 krabber per dag i teinene.
b)
Den 30. dagen (av 60) ligger 5 dager "inn" i klassen [40,60> krabber. Vi antar at antall krabber funnet de 15 dagene i klassen [40,60> er jevnt fordelt i klassen. Tar klassebredden delt på antall dager i klassen, ganger 5:
Medianen vi være $\frac{20}{15}\cdot 5 = 20\cdot \frac{1}{3} \approx 7$ krabber "inn" i klassen, altså 47. Stian kan altså ha rett.
c)
Det er ikke sikkert at antall krabber funnet de 15 dagene i klassen [40,60> er helt jevnt fordelt. Det kan like gjerne være at de fant 59 krabber i 15 dager. Dette vet vi ikke, men kanskje Sebastian har en formening om det? Han kan altså ha rett, men vi vet det ikke sikkert.
d)
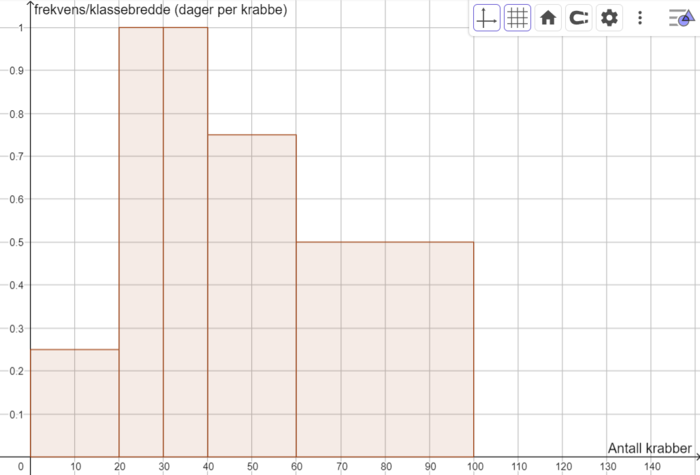
| Antall krabber | Klassebredde (b) | Antall dager (f) | Histogramhøyde (f/b) |
|---|---|---|---|
| [0,20> | 20 | 5 | 0,25 |
| [20,30> | 10 | 10 | 1 |
| [30,40> | 10 | 10 | 1 |
| [40,60> | 20 | 15 | 0,75 |
| [60,100> | 40 | 20 | 0,5 |
Siden dette er del 1, må du tegne histogrammet for hånd.
Oppgave 6
a)
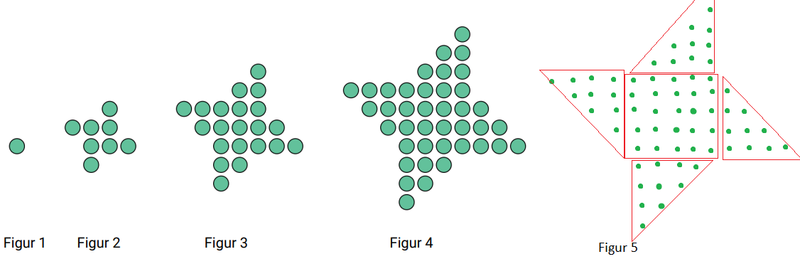
Jeg tegner figur 5 ved å følge mønsteret, og finner 65 sirkler i figur nr. 5.
Jeg tenker meg at figuren består av et kvadrat i midten, som har $5^2= 25$ sirkler. Den har i tillegg 4 trekanter, som hver har $\frac{4\cdot 5}{2}=10 $ sirkler. Til sammen har figuren $25+10\cdot 4=65$ sirkler.
b)
Jeg følger logikken fra oppgave a). Figur nr. n vil ha et kvadrat i midten, med $n^2$ sirkler. Den vil i tillegg ha 4 trekanter som hver har $\frac{(n-1)n}{2}$ sirkler. Til sammen har figuren $n^2 + 4\cdot \frac{(n-1)n}{2} = n^2 + 2n(n-1) = n^2 + 2n^2 -2n = 3n^2 - 2n $ sirkler. Det kan også skrives som $(3n-2)n$ sirkler.
DEL 2
Oppgave 1
a)
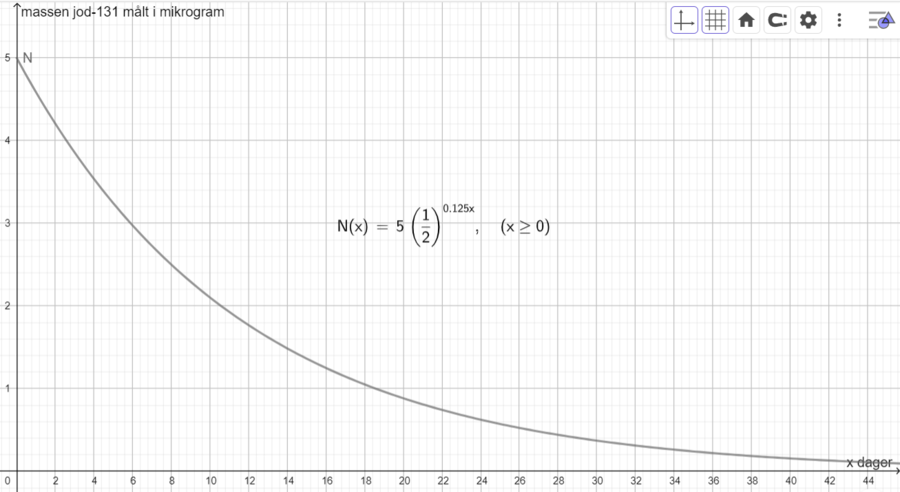
$N(x)=5,0\cdot\frac{1}{2}^{0,125x}$
$N(0)=5,0\cdot\frac{1}{2}^{0} = 5,0 \cdot 1 = 5,0$
Massen jod-131 som er i beholderen i utgangspunktet er 5,0 mikrogram.
b)
c)
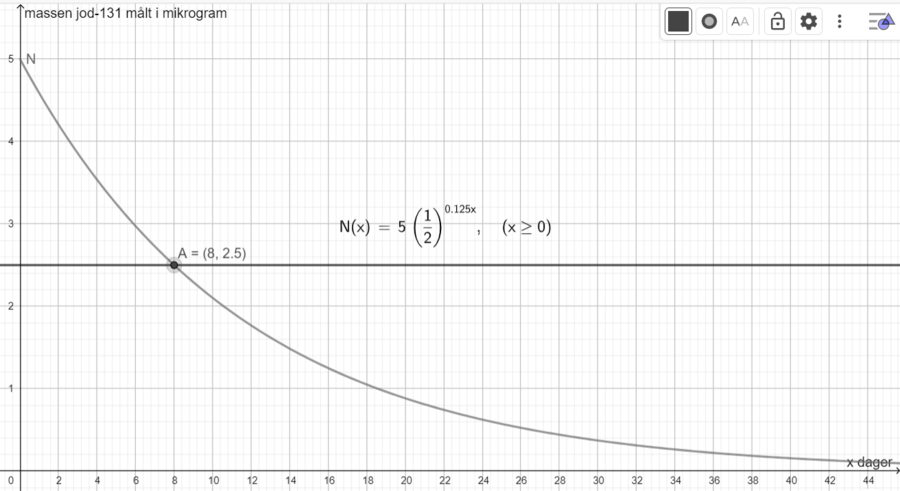
Tegner linjen y=2.5 og bruker "skjæring mellom to objekter" for å finne skjæringspunktet mellom linja og grafen til N. Finner en halveringstid på 8 dager (se punkt A).
d)
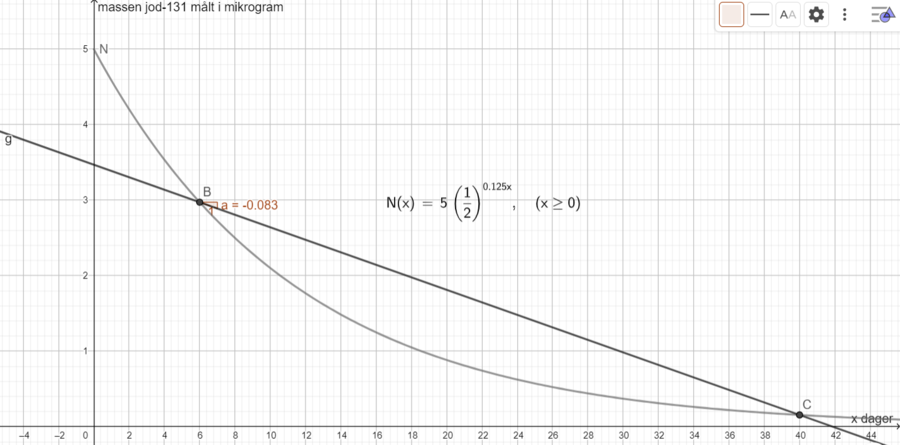
Tegner punktene B=(6,N(6)) og C=(40,N(40)). Lager en linje mellom de to punktene ved å bruke knappen "Linje". Bruker knappen "Stigning" til å finne stigningstallet til linja. Stigningstallet er -0.083 mikrogram per dag. Dette er den gjennomsnittlige vekstfarten fra dag 6 til dag 40. Det forteller oss at massen jod-131 minker med gjennomsnittlig 0,083 mikrogram per dag mellom den 6. og den 40. dagen.
e)
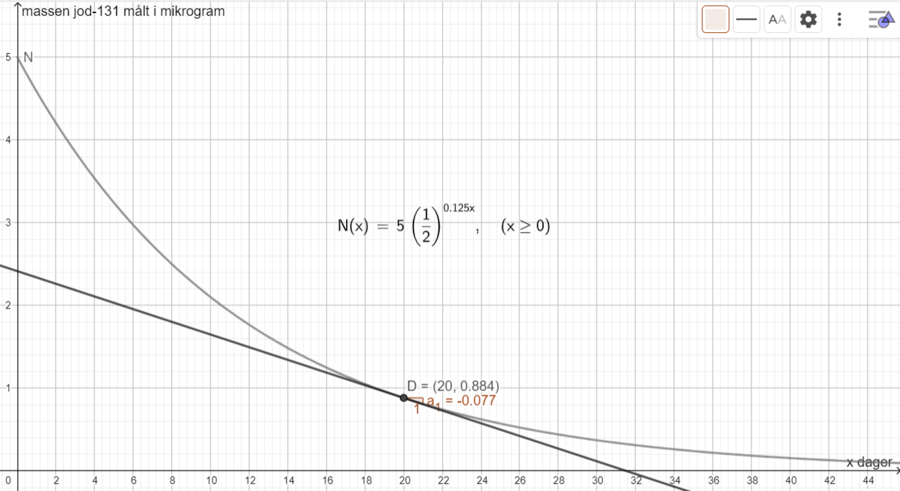
Lager punktet D=(20,N(20)) og bruker knappen "Tangenter" til å finne tangenten til grafen N i punktet D. Bruker knappen "Stigning" til å finne stigningstallet, som er -0.077 mikrogram per dag. Det forteller oss at den 20. dagen, så synker massen jod-131 med en fart på 0.077 mikrogram per dag.
Oppgave 2
a)
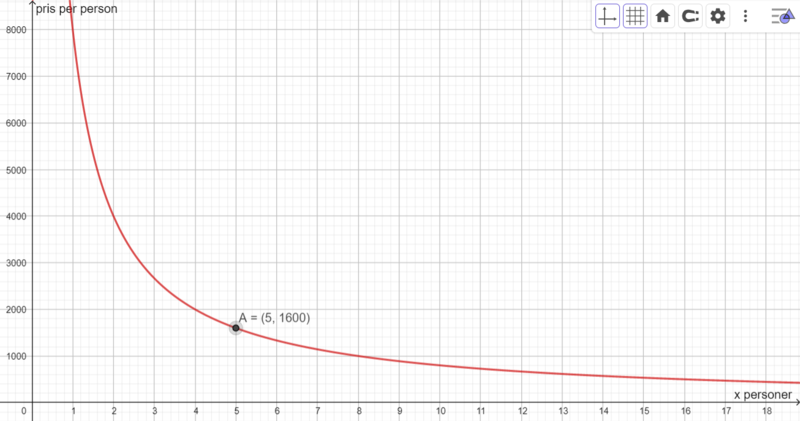
Dette er en omvendt proporsjonal sammenheng. Modellen som jeg tegner i Geogebra blir:
$f(x)=\frac{8000}{x}$
Punktet A=(5,1600) forteller at dersom 5 personer blir med på hytta, må hver person betale 1600 kroner.
b)
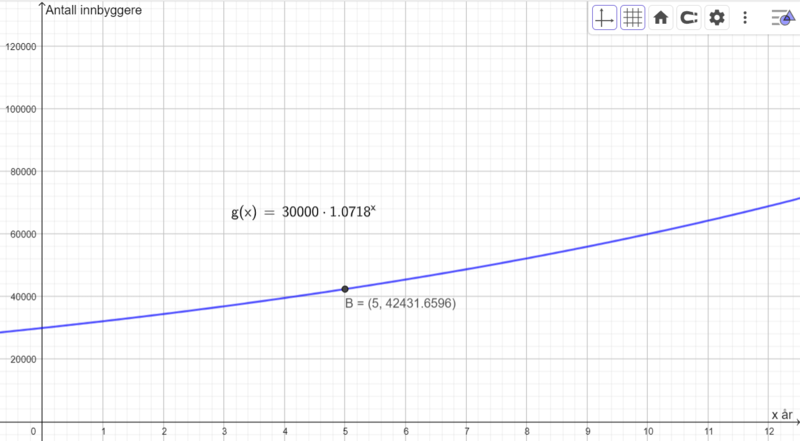
Bruker CAS i Geogebra til å finne prosent årlig vekst (det er også mulig å finne ved prøving og feiling). Finner en vekst på ca. 7,18 % per år. Vekstfaktoren blir da 1.0718, og den eksponentielle modellen blir:
$g(x)=30000\cdot 1.0718^x$
Punktet B=(5,42431) forteller oss at i starten av det 5. året, så er antall innbyggere 42431 personer, ifølge modellen.
Oppgave 3
$G = \frac{410000}{1,07^4\cdot 1,025^3\cdot 0,96^3}$
$G \approx 328294$
Verdien av Trines andel i fondet for 10 år siden var omtrent 328 294 kroner.
Oppgave 4
a)
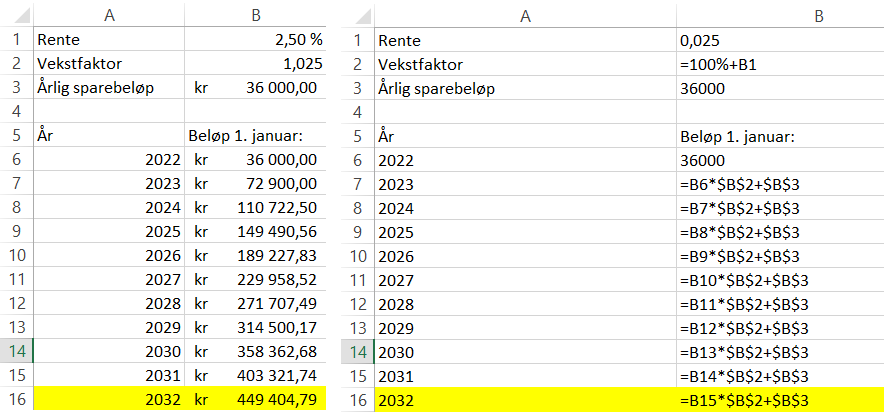
Oppgaven kan løses i CAS, men regneark er også nokså egnet. Jeg viser med regneark, siden CAS ikke er en obligatorisk del av dette faget.
1. januar 2032, vil Amalie ha 449 404,79 kroner på konto.
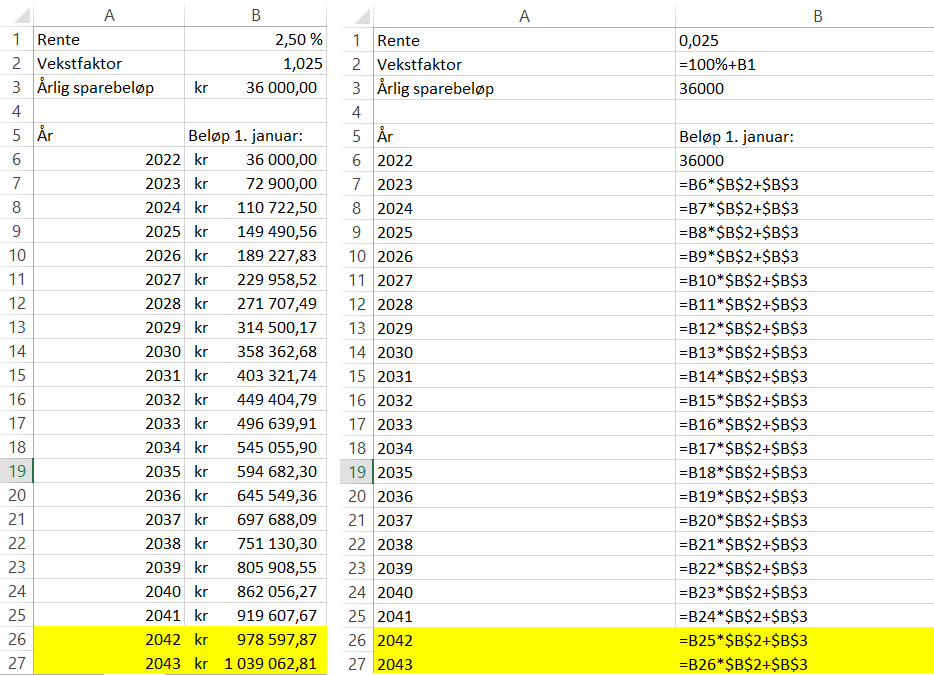
b)
Jeg drar formlene videre nedover regnearket, og finner at beløpet på konto passerer 1 000 000 kroner i løpet av 2042 (siden beløpet er passert 1. januar 2043, selv før det settes inn 36000 kr på konto).
Oppgave 5
a)
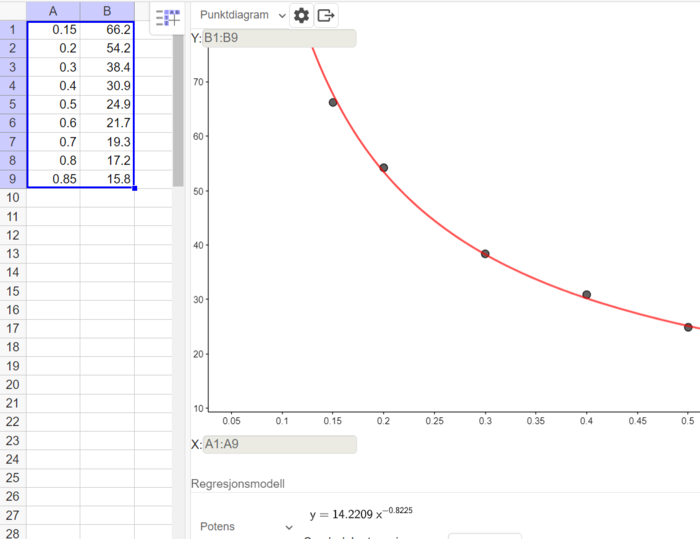
Bruker regresjonsanalyse i Geogebra, og velger en potens-modell.
I modellen $T(x)=a\cdot x^b$, er $a=14.22$ og $b=-0.8225$
b)
Løser oppgaven med CAS i Geogebra, men det finnes flere løsningsmetoder.
Når fallhøyden øker med 40 %, avtar tiden med ca. 24,1 %.
Oppgave 6
a)
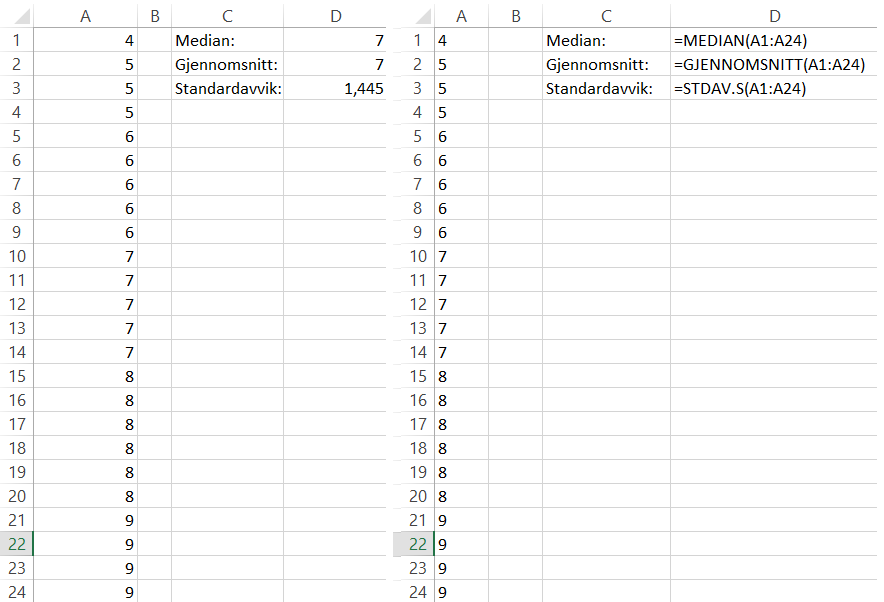
Løser oppgaven i Excel.
b)
Ola får en lavere median enn Kari, som vil si at han har kommet for sent mindre enn 7 minutter minst halvparten av gangene.
Ola får et høyere gjennomsnitt enn Kari, som vil si at han har kommet ganske mye for sent minst én gang.
Ola har et høyere standardavvik enn Kari, som vil si at antall minutter han kommer for sent avviker mer fra gjennomsnittet hans, enn det gjør for Kari.
Totalt sett kan vi si at Ola har kommet flere ganger litt for sent (under 7 minutter) enn Kari, men også har større "rekord" i antall minutter for sent enn Kari (f.eks. mer enn 10 minutter, eller enda mer).
Oppgave 7
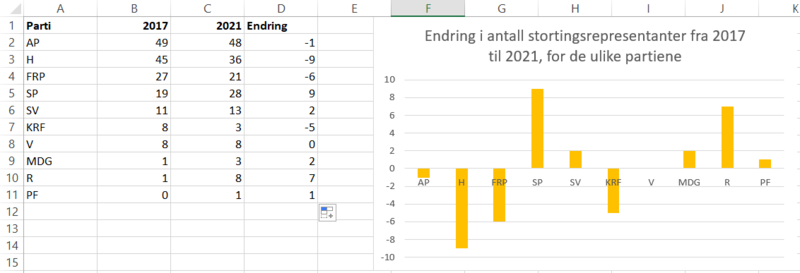
Bruker Excel til å regne ut endringen i antall stortingsrepresentanter for hvert parti fra 2017 til 2021, og til å fremstille et søylediagram som viser denne endringen. Jeg velger søylediagram fordi det er mest visuelt forklarende. Det gjør det enkelt å se endringer i antall representanter for hvert parti.
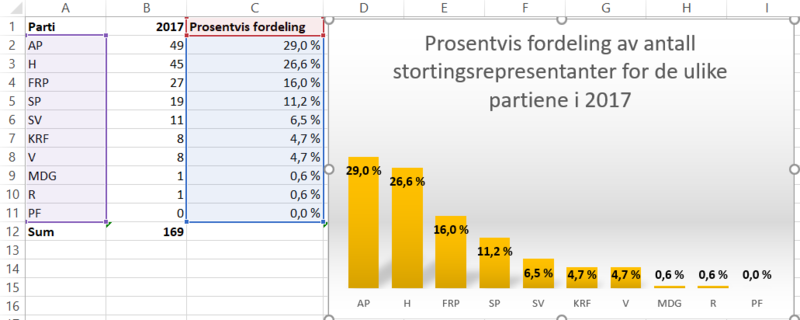
Bruker Excel til å regne ut prosentvis fordeling av representanter fra hvert parti i 2017 (ved å ta antallet i et parti, dele på det totale antall representanter, ganger 100%). Velger igjen et søylediagram, fordi jeg mener det gjør det lettest å se fordelingen. I et sektordiagram blir de minste partiene nesten ikke synlige.
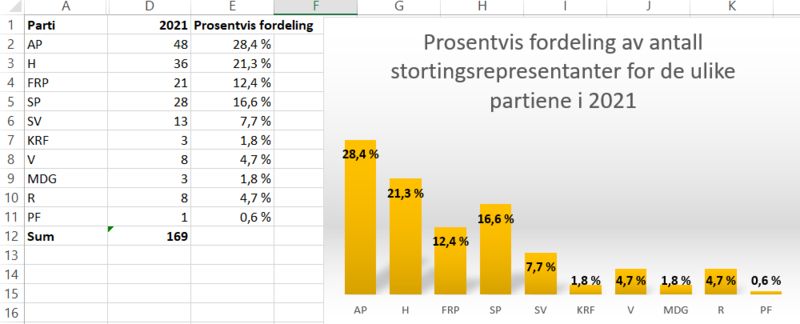
Gjentar prosessen for partiene i 2021.