2P 2013 høst LØSNING
DEL EN
Oppgave 1
Rangerer verdiene i stigende rekkefølge:
0, 0, 0, 0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 7, 11, 28, 32
a)
Median: Det er 20 verdier. Median blir da gjennomsnittet av verdi nr. 10 og nr. 11. Begge disse verdiene er 2, så median er 2.
Gjennomsnitt $ = \frac {0+0+0+0+0+0+1+1+1+2+2+2+3+3+3+4+7+11+28+32}{20}= \frac{100}{20} = 5$
Typetall: Det er fles elever (6) med null dagers fravær. 0 er derfor typetallet.
b)
Vi ser at 4 av 20 elever bidrar betydelig til å trekke opp gjennomsnittet. 12 elever har et fravær på median eller lavere. Det er derfor naturlig å bruke median som sentralmål.
Oppgave 2
$3,2 \cdot 10^8 \cdot4,0 \cdot10^{-3} = \\3,2 \cdot 4,0 \cdot 10^{8+(-3)} =\\ 12,8 \cdot 10^5 = \\1,28 \cdot 10^6$
Oppgave 3
a)
$(2^2)^{-3} \cdot 4^4= \\2^{-6} \cdot (2^2)^4 = \\ 2^{-6+8} =\\2^2=4$
b)
$(\frac32)^2 \cdot \frac{(2^3)^2 \cdot 3^{-1}}{6} = \\ \frac{3^2 \cdot 2^6 \cdot 3^{-1}}{2^2 \cdot 2 \cdot 3} = \\ 3^{2-1-1} \cdot 2^{6-3} = 2^3 =8$
Oppgave 4
$ R(t) = 200 000 \cdot 1,0465^t - 200 000 \\ R(5)= 200 000 \cdot 1,0465^5 - 200 000$
R(t) er et uttrykk for rentepengene etter t år. 200 000 er innskuddet, 1,0465 er vekstfaktoren, og t er tiden i år, i dette tilfellet 5. Man må trekke fra innskuddet på 200 000 kroner for å finne rentepengene.
Oppgave5
a)
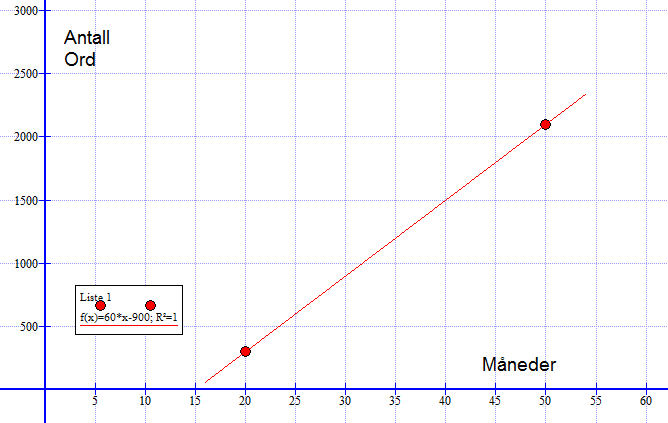
Her må du plotte punktene og tegne grafen for hånd. vi bruker digitalt verktøy.
b)
Fra figuren i a ser man at et barn på 35 måneder kan ca. 1200 ord.
c)
$f(x)= 60x - 900$
Barnet lærer ca. 60 nye ord per måned. -900 er en korreksjon fordi barnet ikke lærer noen ord de første månedene.
De fleste voksen har trolig et aktivt ordforråd på mellom 5000 - 10.000 ord, passivt muligens det dobbelte. Det betyr at for de fleste av oss vill lærekurven flate ut. Dette har trolig sammenheng med utdannelse og andre sosiale faktorer. Det påståes at Wergeland behersket ca 50.000 ord. Dersom det stemmer var det ingen utflating!! Bokmålsordboka består til sammenligning av ca. 65.000 ord, nynorskordboka over 90.000 ord. Modellen gjelder selvsagt ikke før barnet kan prate. I følge denne modellen skjer det ved ca. 15 måneder.
Oppgave 6
| Lommepenger ( kroner) | Antall elever $f$ | Klassemidpunkt $x_m$ | Klassesum $f \cdot x_m$ |
| $[0 , 300\rangle $ | $30$ | $150$ | $4500$ |
| $[300 , 600\rangle $ | $15$ | $450$ | $6750$ |
| $[600 , 900\rangle $ | $5$ | $750$ | $3750$ |
| $N=50$ | $S=15000$ |
For å regne ut gjennomsnittet i klassedelt materiale må vi anta at gjennomsnittet i hvert av de tre intervallene ligger på klassemidpunktet. Slik trenger det ikke å være, men det er det beste vi har, fordi vi vet bare at 30 elever ligger mellom ingen lommepenger og opp til 299,99 kroner. Dersom disse 30 fordeler seg jevnt i intervallet blir gjennomsnittet for intervallet tilnærmet riktig, men vi har jo ingen garanti for at det er slik. Men, på grunnlag av antagelsen:
Gjennomsnitt $\frac SN = \frac {15000}{50} = 300$ Kr.
Oppgave 7
$f(x)= 300000 \cdot 0,9^x$
Vekstfaktoren er 0,9 hvilket betyr at noe avtar med 10% per tidsperiode (sek, min, dager, måneder, år, etc). Startverdien er 300 000. Dersom du kjøper en motorbåt til 300 000 kroner er det ikke usannsynlig at den får et verditap på 10% per år. Da kan denne modellen brukes.
Oppgave 8
a)
| $2^5$ | $2^4$ | $2^3$ | $2^2$ | $2^1$ | $2^0$ |
| 32 | 16 | 8 | 4 | 2 | 1 |
$11_{10} = 8+0+2 + 1 = 1011_{2} \\ 22_{10} = 16 +0 +4+2+0 = 10110_2 \\ 44_{10} = 32 + 0 + 8 + 4 + 0 + 0 = 101100_2$
b)
I totallsystemet dobler man ett tall ved å legge til null på enerplassen (høyre side). Da skyves alle siffer ett hakk mot venstre og tallet øker med en faktor to.
c)
Vi formulerte en regel for totallsystemet i b. Fra titallsystemet vet vi at vi tidobler ved å legge til en null på enerplassen, feks fra 10 til 100. Den samme logikken bør kunne anvendes i tretallsystemet.
$121_3 = 9 + 6 + 1 = 16_{10} \\ 1210_3 = 27+18+3+0 = 48_{10}$
Vi observerer at vår lille hypotese ble bekreftet. En tredjedel av $ 120010_3$ er da $12001_3$
DEL TO
Oppgave 1
Oppgave 2
Oppgave 3
a)
$E = mc^2 \\ E = 0,010kg \cdot (3,0 \cdot 10^8)^2 \\ E = 1,0 \cdot 10^{-2} \cdot 9,0 \cdot 10^{16} = 9 \cdot 10^{14} J$
0,010 kg masse gir $9,0 \cdot 10^{14}$ Joule.
b)
$m = \frac {E}{c^2} = \frac{9 \cdot 10^{10}}{9 \cdot 10^{16}} = 10^{-6} = 0,000001 kg = 0,001 gram$
0,001 gram masse må forsvinne for å dekke energibehovet til en norsk husstand ett år.
Oppgave 4
a)
1) Lineær modell
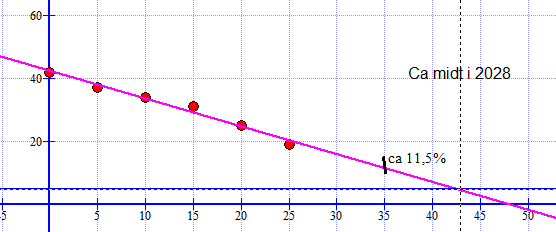
$f(x) = -0,88x + 42,3$
2) Eksponentiell modell
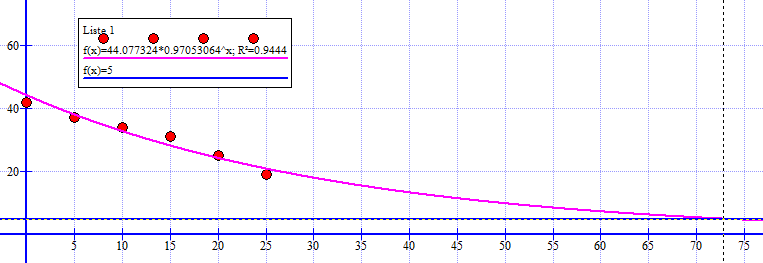
$f(x) = 44 \cdot 0,97^x$
b)
2020 tilsvarer x = 35:
$f(x) =-0,88x + 42,3 \\ f(35)= -0,88 \cdot 35 +42,3 = 11,5 $
I følge den lineære modellern røker 11,5% av norske menn i 2020.
$f(x)= 44\cdot 0,97^x \\ f(35)=44 \cdot 0,97^{35} = 15.2 $
I følge den eksponentielle modellen vil 15,2% av norske menn røke i 2020.
c)
Mindre enn 5% menn som røyker:
$f(x)=5$
- Lineær modell:
$f(x)=5 \\ -0,88x +42,3 = 5 \\ -0,88 = -37,3 \\ x= \frac{-37,3}{-0,88} = 42,4$
42,4 + 1985 = 2027,7
Ved utgangen av 2027 vil mindre enn 5% av norske menn røke, i følge den lineære modellen.
- Eksponentiell modell:
$f(x)=5 \\ 44 \cdot 0,97^x = 5 \\$
Utregningen her ble litt vannskelig for 2P, det er nok best å løse det grafisk og å lese av i koordinatsystemet. Finner da at x = 71,4, dvs. mindre enn 5% mannlige røkere i løpet av år 2056.
d)
I følge den lineære modellen kommer alle norsk menn til å slutte å røke. Hvert år slutter det samme antall personer å røke. Det er ikke realistisk .
Den eksponentielle modellen sier at ca 3% av denne gruppe røkere slutter hvert år. Dette er en mer realistisk modell, med et større gyldighetsområde.
Oppgave 5
a)
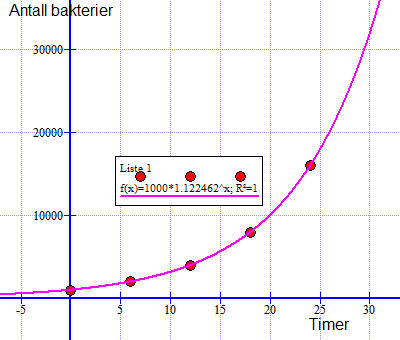
24 timer er 4 doblinger: 1000 - 2000 - 4000 - 8000 - 16 000, altså 16 000 bakterier etter 24 timer.
b)
Bruker modellen fra opg. a.
$f(x) = 1000 \cdot 1,122^x $
c)
Vekstfaktoren i b er 1,122, dvs. at økningen per time er 12,2%
d)
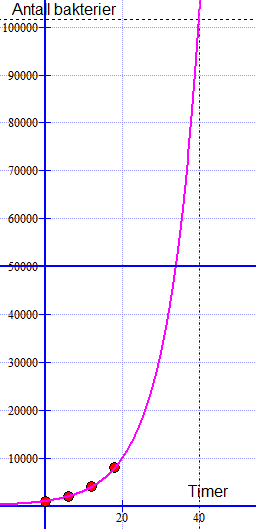
Fra figuren ser man at det etter 40 timer vil være ca. hundre tusen bakterier (101590). 50000 bakterier når man etter 33,9 timer.
Oppgave 6
a)
| Tid ( minutter) | Antall elever $f$ | Klassemidpunkt $x_m$ | Klassesum $f \cdot x_m$ |
| $[10 , 20\rangle $ | $8$ | $15$ | $120$ |
| $[20 , 30\rangle $ | $6$ | $25$ | $150$ |
| $[30 , 40\rangle $ | $4$ | $35$ | $140$ |
| $[40 , 50\rangle $ | $1$ | $45$ | $45$ |
| $[50 , 60\rangle $ | $3$ | $55$ | $165$ |
| $[60 , 70\rangle $ | $3$ | $65$ | $195$ |
| $[70 , 80\rangle $ | $3$ | $75$ | $225$ |
| $[80 , 90\rangle $ | $2$ | $85$ | $170$ |
| $N=30$ | $S=1210$ |
b)
Gjennomsnitt: $gj = \frac SN = \frac{1210}{30} = 40,3$
Elevene bruker i gjennomsnitt 40,3 minutter på å reise til og fra skolen.
c)
Åtte av tretti brukere mere enn 60 minutter, dvs 22 av 30 bruker mindre enn 60 minutter, dvs. ca. 73,3%
Oppgave 7
a)
Karaktergjennomsnitt multiplisert med 10: $ gj = \frac{2+2+2+3+3+3+3+3+3+4+4+4+4+4+4+4+4+4+4+5+5+5+5+5+6}{25} \cdot 10 = 3,8 \cdot 10 = 38$
I tillegg har han 4 alderspoeng, 2 poeng for førstegangstjenesten og 1,5 ekstrapoeng for fag: 38,0 + 4,0 + 2 + 1,5 = 45,5 poeng.
b)
Neste år vil han ha 9,5 poeng i tillegg til karaktergjennomsnittet: 50,7 - 9,5 = 41,2.
Han må ha et karaktergjennomsnitt på 4,12.
c)
Han må ha et snitt på 4,12
Han har et snitt på 3,8
Han mangler 4,12 - 3,8 = 0,32
Dersom han forbedrer ett fag med en karakter er det $\frac {1}{25} = 0,04$
Han må altså forbedre $\frac{0,32}{0,04} = 8$ fag, stakkars gutt!!