1T 2017 høst LØSNING
Diskusjon av denne oppgaven på matteprat
Løsningforslag som video på UDL.no
Fullstendig løsningsforslag som pdf laget av Lektor Nilsen
Forslag til fasit (ikke løsningsforslag) laget av mattepratbruker Markus: del 1 del 2
Har du et alternativt løsningsforslag du ønsker å dele? Send inn til cosinus@matematikk.net så legger vi det ut!
DEL EN
Oppgave 1
$\frac{120 \cdot 25000}{0,15} =\frac{1,2 \cdot 10^2 \cdot 2,5 \cdot 10^4}{1,5 \cdot 10^{-1}} = 2,0 \cdot 10^{2+4-(-1)} = 2,0 \cdot 10^{7}$
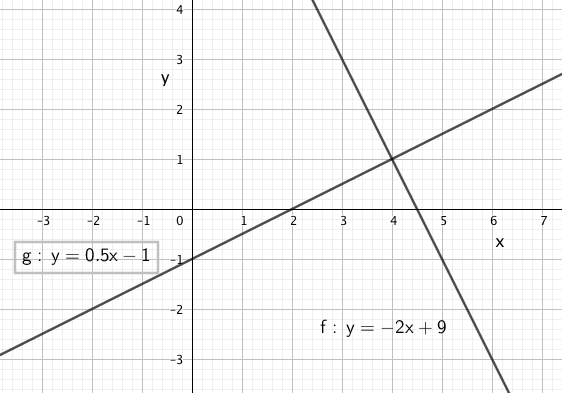
Oppgave 2
Fra figuren ser man at løsningen er x = 4 og y = 1.
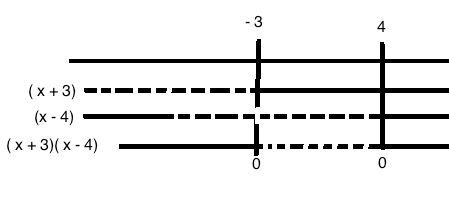
Oppgave 3
$x^2-x- 12 \leq 0$
Faktoriserer (abc formel eller koeffisientmetode) og får:
$(x-4)(x+3) \leq 0$
Tegner fortegnsskjema:
$x \in [-3, 4]$
Oppgave 4
$0< Sin (73^{\circ})< 1 \\ Tan(45^{\circ}) =1 \\ln 1 =0 \\ lg(10^{- \frac 14} = - \frac 14$
Rekkefølge blir da: $ lg(10^{- \frac 14}), \quad ln1, \quad Sin (73^{\circ}), \quad Tan(45^{\circ}) $
Oppgave 5
$lg(x + \frac{1}{25})= -2 \\ x + \frac{1}{25} = 10^{-2} \\ x= \frac{1}{100}- \frac{1}{25} \\ x= - \frac{3}{100} $
Oppgave 6
$\frac{\sqrt x +\sqrt x + \sqrt x}{\sqrt x \cdot \sqrt x \cdot \sqrt x} = \frac{3 \sqrt x}{x \sqrt x} = \frac{3}{x}$
Oppgave 7
$ \frac {\sqrt{75}}{\sqrt{30}} \cdot 5^{-1} \cdot 10^{\frac 12} + 8^{\frac 13} = \\ \frac {5 \sqrt{3}}{\sqrt{3} \sqrt{10}} \cdot \frac 15 \cdot \sqrt{10} + 2 = \\ 1+2 =3 $
Oppgave 8
Lineær funksjon: y= ax + b, stigningstallet er det samme i hele definisjonsområdet, altså $a = f'(x) = f'(2)= 3$
Vi har punktet (2, 4) og får:
$y = 3x + b \\ 4 = 3 \cdot 2 + b \\ b= -2$
som gir utrykket
f(x)= 3x -2
Oppgave 9
a)
$3x^2-9x = 3x(x - 3)$
b)
$\frac{x}{x-2} + \frac{2x}{x-3} - \frac{2x}{x^2-5x+6} \\ = \frac{x}{x-2} + \frac{2x}{x-3} - \frac{2x}{(x-3)(x-2)} \\= \frac{x(x-3)}{x-2} + \frac{2x(x-2)}{x-3} - \frac{2x}{(x-3)(x-2)} \\ = \frac{x^2-3x+2x^2-4x-2x}{(x-3)(x-2)} \\ = \frac{3x^2-9x}{(x-3)(x-2)} \\ = \frac{3x}{x-2}$
Oppgave 10
a)
A - Eleven går i 2A
$\bar{A}$ - Eleven går i 2B
B - Eleven har biologi
$\bar{B}$ - Eleven har ikke biologi
$P(B) = P(A) \cdot P(B|A) + P( \bar{A}) \cdot P(B| \bar{A}) = 0,5 + 0,25= 0,75$ altså 75%.
b)
$P(A|B) = \frac{P(A) \cdot P(B|A)}{P(A) \cdot P(B|A) + P( \bar{A}) \cdot P(B| \bar{A})} = \frac{0,5}{0,75} = \frac 23$
Det er to tredjedels sjanse for at tilfeldig elev med biologi går i 2A.
Oppgave 11
a)
$f(-1)= (-1)^4-2(-1)^3+2= 5 \\ f(1)= 1^4 - 2 \cdot 1^3 +2 = 1$
Endring i y verdi er -4 og endring i x verdi er 2. Gjennomsnittlig stigning blir da
$\frac{\Delta y}{\Delta x} = \frac{-4}{2} = -2$
b)
$f(x)= x^4-2x^3+2\\ f'(x)= 4x^3-6x^2 = 2x^2(2x-3)$
Den deriverte er null for x = 0 og f(0) = 2
$f'(-1)= -10 \\ f'(1)=-2 $
Funksjonen er strengt avtagende på begge sider av x=0. derfor er (0,2) et terassepunkt.
Oppgave 12
a)
$f(x)=x^3-6x^2+12x-8 \\ f'(x)= 3x^2-12x+12 $
b)
$y = ax + b \\ a = f'(1) = 3-12+12 =3 \\ f(1)= 1-6+12-8 = -1 \\ y = ax + b \\ -1 = 3 +b \\ b= -4 \\ y=3 x-4$
c)
Ja, den har en til. $f'(x)=3 $ gir også løsning for x = 3. Funksjonen har en parallell tangent i punktet (3, f(3)).
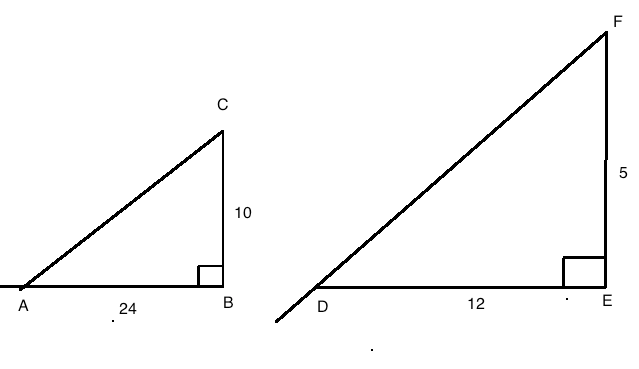
Oppgave 13
Trekant DEF er mindre enn ABC, men siden dette er en skisse er det ok.
Oppgave 14
a)
Radius i sirkelene er a.
Ser på figuren som to "delvise" sirkler og får at omkretsen blir:
$O= 2 \pi a + 2 \pi a = 4 \pi a$
b)
Har seks kvarte sirkler med radius a: $\frac 64 \pi a^2$
Plusser på arealet av resterende skravert område som er rektangelet 2a ganger a minus halvsirkelen som ikke er med:
$ A = \frac 64 \pi a^2 +( 2a \cdot a - \frac 12 \pi a^2) \\ A= \pi a^2 + 2a ^2 = a^2( \pi + s) $
DEL TO
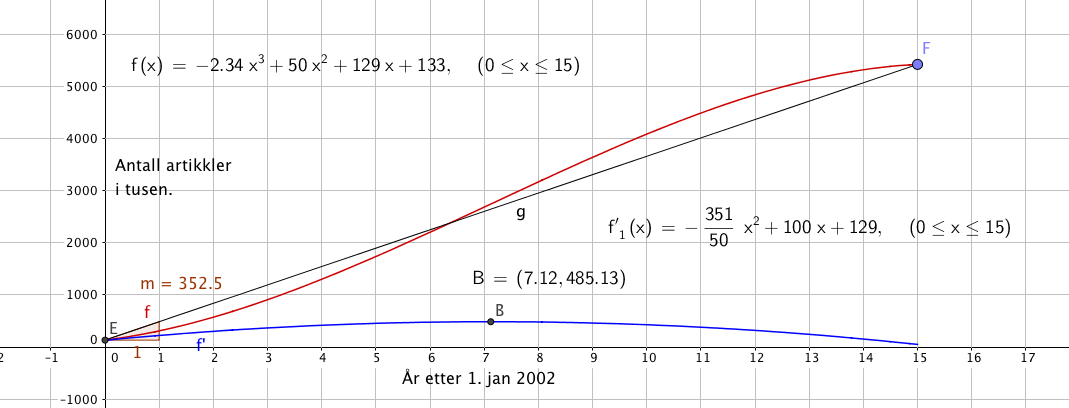
Oppgave 1
a)
b)
Den gjennomsnittlige vekstfarten disse 15 årene er 352,5. Det betyr at antall artikler øker med ca 352,5 tusen artikler per år i denne perioden.
c)
Se figur i a.
d)
Toppunkt til den deriverte er ( 7.12 , 485) og er et utrykk for hvor grafen vokser raskest, og med hvor mye. Den momentane veksten er størst i februar 2009.
Oppgave 2
a)
Det er totalt 12 kuler og 5 er ødelagt, dvs 7 er ikke: Sannsynlighet for to kuler som ikke er ødelagt:
$P(ok) = \frac{7}{12} \cdot \frac{6}{11} = \frac{7}{22}$
b)
Alternativet til minst en ødelagt kule er at begge er ok. Denne sannsynligheten fant vi i a. Sannsynligheten for minst en ødelagt blir da: P (minst en ødelagt $= 1- \frac{7}{22 } = \frac{15}{22}$.
Oppgave 3
Bruker sinussetningen til å finne hypotenusen i trekanten som har en vinkel på 36 grader:
$\frac{140m}{sin 14} = \frac{x}{sin 130} \\ x = 443,3m$
Bruker så definisjonen på sinus til å finne høyden h: $sin (36) = \frac{h}{443,3m} \\ h = 260,6m$
Oppgave 4
a)
b)
Oppgave 5
a)
Bunnpunkt eller minimumspunkt. Vi finner den deriverte og setter den lik null. X verdien setter vi inn i funksjonsuttrykket, så har vi punket.
$f(x) = 2x^2 - 7x +3 \\ f'(x)= 4x-7 \\ f'(x)=0 \\ 4x-7 = 0 \\ x= \frac 74$
$ f( \frac74) = 2 \cdot (\frac 74)^2 - 7 \cdot \frac 74 +3 = \frac{49-98+24}{8} = \frac{25}{8} $
Dersom man er lur kan man jo også gjøre den på CAS:
b)
c)
Definerer punktene T og S.
Løser likningen 5 og 6 og finner at x koordinaten P ligger midt mellom S og T.