1T 2012 høst LØSNING
DEL EN
Oppgave 1
$a = -2$ og punkt. $(3,0)$
$0 = -2 \cdot 3 + b \\ b= 6$
dvs:
$y=-2x+6$
Oppgave 2
<math>lg(2x+3) = 1 \\ 10^{lg(2x+3)} = 10^1 \\ 2x+3 =10 \\ x= \frac 72</math>
Oppgave 3
<math>\frac{(2x)^3x^2}{2^5x^{-1}} = 2^{3-5}x^{3+2+1}= \frac{x^6}{4}</math>
Oppgave 4
<math>\frac{x^2+6x+9}{x^2-9} = \frac{(x+3)(x+3)}{(x+3)(x-3)} = \frac{x+3}{x-3}</math>
Oppgave 5
<math> (\sqrt2 + \sqrt8)^2 = 2+2\sqrt2\sqrt8+8 = 18</math>
Oppgave 6
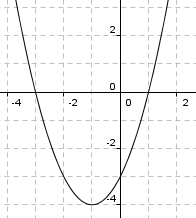
a)
Nullpunkter:
f(x) = 0
<math> x^2+2x-3 =0 \\ x= \frac{-2 \pm\sqrt{4+4 \cdot 3}}{2} \\ x=-3 \quad \vee \quad x=1</math>
b)
<math>f'(x) = 2x+2 \\ f'(x) = 0 \\ x= -1 \\ f(-1)=-4</math>
f har et ekstremalpunkt i (-1,-4). Dette er et minimumspunkt da den deriverte er negativ for verdier mindre enn -1, og positiv for større verdier.
c)
Oppgave 7
<math>(x+5)(x+3)-(x+5)(2x+7)=0 \\ (x+5)(x+3-2x-7)=0 \\ (x+5)=0 \quad \vee \quad -x-4=0 \\ x=-5 \quad \vee \quad x=-4</math>
Oppgave 8
a)
| Bio | <math>\bar{Bio}</math> | Sum | |
| Fys | <math>5</math> | <math>7</math> | <math>12</math> |
| <math>\bar{Fys}</math> | <math>9</math> | <math>4</math> | <math>13</math> |
| Sum | <math>14</math> | <math>11</math> | <math>25</math> |
b)
<math>P(fys\quad og \quad bio) = \frac{5}{25} = \frac 15</math>
c)
<math>P(fys\quad | \quad bio) = \frac{5}{14} </math>
Oppgave 9
a)
<math>SinA = \frac{12}{13} \\ CosA = \frac{5}{12}</math>
b)
<math>(SinA)^2+(CosA)^2 = (\frac{12}{13})^2 + (\frac{5}{13})^2 = \frac{144+25}{169} = 1</math>
c)
<math>a^2+c^2 = b^2 \\ \frac{a^2+c^2}{b^2}=1 \\ \frac{a^2}{b^2} + \frac{c^2}{b^2}= 1 \\ (\frac{a}{b})^2 + (\frac{c}{b})^2=1 \\ \frac ab = SinA \quad \wedge \quad \frac cb = CosA \\ (SinA)^2 + (CosA)^2 = 1 </math>
Oppgave 10
<math> x^2 +x^2 = 16 \\ x= \sqrt 8</math>
Sidene i kvadratet har lengden kvadratroten av åtte.
Areal kvadrat = 8
Areal sirkel =<math>\pi r^2 = \pi (\frac{\sqrt8}{2})^2 = 2\pi</math>
Areal av skravert område blir: areal kvadrat - areal sirkel = <math>8-2\pi</math>
DEL TO
Oppgave 1
a)
<math> \frac{1}{R}= \frac{1}{R_1} + \frac{1}{R_2}\\ \frac{1}{R}=\frac{1}{5}+\frac{1}{7}\\ \frac{1}{R}=\frac{7}{35}+ \frac{5}{35}\\ \frac{1}{R} =\frac{12}{35}\\ 12R = 35 \\ R=\frac{35}{12} </math>
b)
<math> R_2 = 2R_1 \\\frac{1}{R}=\frac{1}{R_1} +\frac{1}{2R_1}\\ \frac{1}{R}= \frac{2}{2R_1}+\frac{1}{R_1} \\ \frac{1}{R} = \frac{3}{2R_1} \\ 3R = 2R_1 \\ R = \frac{2}{3}R_1 </math>
Oppgave 2
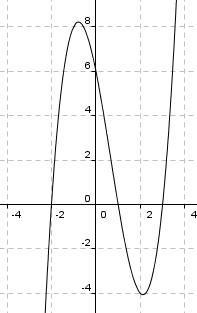
a)
b)
<math>f'(x) = 3x^2-4x-5 \\ f'(1)= 3-4-5 =-6 \\ f(1) = 1-2-5+6 =0 \\ 0 = -6 \cdot 1 + b \\ b= 6 \\ y= -6x+6</math>
c)
<Math>f'(x) = 3x^2-4x-5 \\ f'(x) =2 \\ \Downarrow \\ 3x^2-4x-5=2 \\ 3x^2 -4x - 7 =0 \\ x=-1 \vee x = \frac 73 </Math>
<Math>f(-1)=8 \wedge f( \frac73) = - \frac{104}{27}</Math>
Tangeringspunkter det tangenten har stigning to blir da:
<Math>(-1,8) \wedge (\frac 73, - \frac{104}{27})</Math>
Likningene blir da: <Math>y = ax+b \\ 8=-2+b \\ b =10 \\ y = 2x+10 </Math> og tilsvarende for det andre punktet <Math>- \frac{104}{27} = \frac{2 \cdot 7}{3} + b \\ b= - \frac{230}{27} \\ y =2x- \frac{230}{27}</Math>
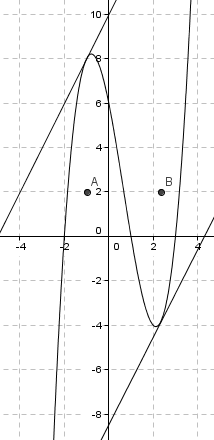
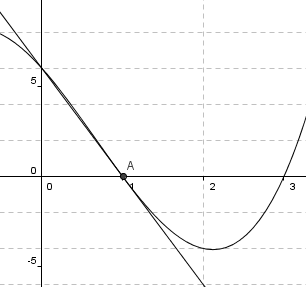
Bruker Geogebra:
(punktene A og B har ingen ting med saken å gjøre, er bare tangeringens x koordinater.)
Oppgave 3
a)
<math>Cos \alpha = \frac {4}{11} \\ \alpha = 68,7^{\circ}</math>
b)
<math>h^2 = 11^2 - 4^2 \\ h = \sqrt{105} \approx 10,2</math>
Oppgave 4
a)
Sannsynlighet for å betale med kort P(kort) = 0,6
Sannsynligheten for at de 10 første kundene betaler med kort:
<math>P = 0,6^{10} = 0,006 = 0,6%</math>
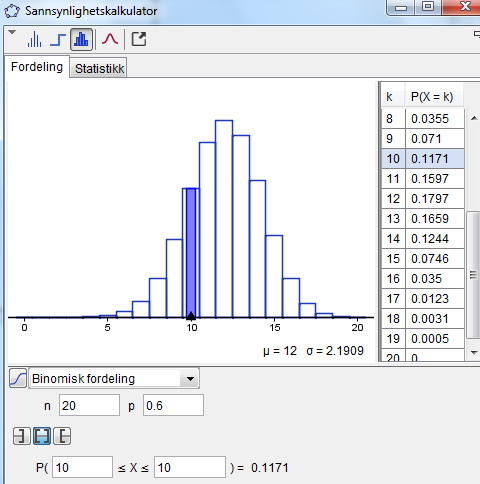
b)
Sannsynligheten for at 10 av de første 20 bilene betaler med kort.
Sannsynligheten er 11,7%
c)
Sannsynligheten for at mer enn 25 av de 50 første bilene betaler med kort:
Sannsynligheten er 90,2%
Oppgave 5
a)
Velger 6 og 7.
<math>6+7+6^2 = 49 \\ 7^2 = 49</math>
Dette ser jo lovende ut..
b)
<math>n+(n+1)+ n^2 = (n+1)^2 \\ n^2 + 2n + 1 = (n+1)^2 \\ (n+1)^2 = (n+1)^2</math>
Oppgave 6
a)
<math>(8-x)^2 =x^2+25 \\ 64-16x+x^2 = x^2+25 \\ -16x = -39 \\ x=2,4</math>
b)
<math> a^2 = b^2 + c^2 - 2bc cosA \\ x^2 = 25+64 - 16x + x^2 - 2\cdot 5 \cdot (8-x) cos 30^{\circ} \\ 7,33x = 19,7 \\ x = 2,7</math>
c)
<math>\frac{SinE}{5,3} = \frac{Sin 30^{\circ}}{2,7} \\ E = 79^{\circ} </math>
Oppgave 7
a)
<Math>4x+h=30 \\h = 30-4x \\ setter \quad h=0 \\ x= \frac{30}{4} \\ x= 7,5 </Math>
dvs.
<Math>0 < x <7,5</Math>
b)
<math>O(x) = x^2 + 4x(30-4x) \\ O(x)=x^2 + 120x - 16x^2 \\ O(x)= -15x^2+120x</math>
c)
<math>O'(x)= -30x+120 \\ O'(x) =0 \\ \Downarrow \\ -30x+120 =0 \\ x =4 </math>
Fire desimeter gir den største overflanten. Da er overflaten:
<math>O(4) = -15 \cdot 4^2 + 120 \cdot 4 = 240</math>
Da er overflaten 240 kvadratdesimeter.