1P 2023 vår LK20 LØSNING

Oppgaven som pdf

Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas

Diskusjon av oppgaven på matteprat

Videoløsning av KublaKan Utdanning

DEL 1

Oppgave 1

Det er 30 kr i prisforskjell mellom de to sjokoladeplatene.

Prisforskjell sammenlignet med prisen på butikken:

$\frac{30}{20}\cdot 100 \% = \frac{3}{2}\cdot 100\% = 1,5 \cdot 100 \% = 150 \%$

Sjokoladeplaten er 150 % dyrere på bensinstasjonen enn på butikken.

Prisforskjell sammenlignet med prisen på bensinstasjonen:

$\frac{30}{50}\cdot 100\% = \frac{60}{100}\cdot 100\% = 0,6\cdot 100\% = 60\% $

Sjokoladeplaten er 60 % billigere på butikken enn på bensinstasjonen.

Marko og Mari har regnet riktig. Den prosentvise prisforskjellen kommer an på hva man sammenligner prisforskjellen med.

Oppgave 2

8 milliarder på standardform: $8\cdot 10 ^9$

2,5 millioner på standardform: $2,5\cdot 10^6$

Antall maur på jorden: $8\cdot 10 ^9 \cdot 2,5\cdot 10^6 = 20 \cdot 10^{9+6} = 20 \cdot 10^{15} = 2 \cdot 10^{16}$

Det er omtrent $2 \cdot 10^{16}$ maur på jorden.

Oppgave 3

a)

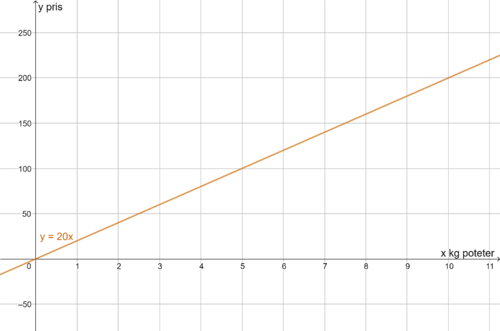
Prisen du må betale for poteter er proporsjonal med antall kg poteter du kjøper. Vi antar at du kjøper poteter i løsvekt med en gitt kilopris, f.eks. 20 kr/kg. Kjøper du 1 kg, koster det 20 kr. Kjøper du 2 kg, koster det 40 kr. osv.

Grunnen til at det er proporsjonale størrelser, er at forholdet mellom disse alltid er det samme (i dette tilfellet, at kiloprisen er lik). Vi har k = y/x.

b)

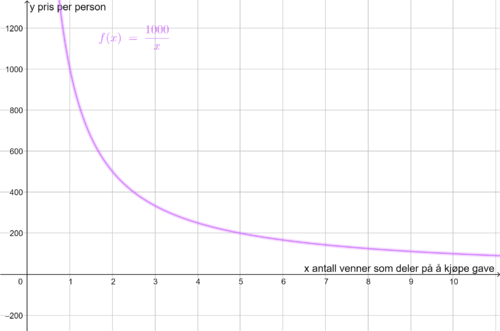
Prisen hver person må betale dersom en gruppe deler på å kjøpe gave til en venn, er omvendt proporsjonal med hvor mange personer som er med på å betale for gaven. Vi antar at gaven koster 1000 kr. Dersom bare 2 venner deler på prisen, må hver person betale 500 kr. Dersom 4 venner deler på prisen, må hver person betale 250 kr. osv.

Grunnen til at det er omvendt proporsjonale størrelser, er at produktet av disse alltid er det samme (i dette tilfellet, at prisen på gaven er fast). Vi har k = x*y.

Oppgave 4

a)

Ut fra tabellen, ser det ut som høyden til Klara stiger jevnt med 7 cm per år, så vi kan lage en lineær modell med 7 som stigningstall.

Vi må finne høyden til Klara da hun var 0 år. Vi antar at hun vokste med 7 cm per år også de fire første årene. Da vokste hun med 28 cm på fire år, og var da 100-28=72 cm ved fødsel (som ikke høres realistisk ut).

Modellen er $f(x) = 7x + 72$, der x er antall år Klara er, og f(x) er høyden til Klara.

b)

$f(19)=7\cdot 19 + 72 = 133 + 72 = 205$

Klara vil ifølge modellen være 205 cm høy når hun fyller 19 år, som ikke høres realistisk ut.

c)

Hvis Klara var 50 cm da hun ble født, er ikke modellen gyldig fra fødselen av.

$f(2)=7\cdot 2 + 72 = 14 + 72 = 86$

Ifølge modellen var klara 86 cm høy da hun var 2 år, som høres høyt ut. Jeg bestemmer at modellen er gyldig fra målingene begynner, fra Klara er 4 år.

$f(14)=7\cdot 14 + 72 = 98 + 72 = 170$

Ifølge modellen vil Klara være 170 cm høy når hun blir 14 år, som høres ut som en realistisk voksen høyde. Jeg bestemmer at modellen er gyldig til hun er 14 år.

Jeg bestemmer at modellen er gyldig fra Klara er 4 år til hun er 14 år. Vi kan uansett ikke vite sikkert hvor høy hun vil bli.

DEL 2

Oppgave 1

a)

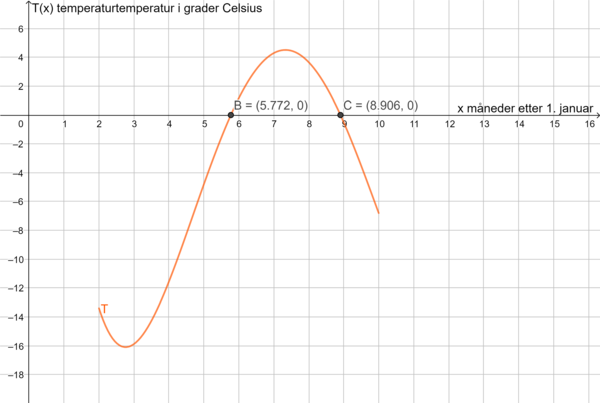
Bruker Geogebra til å tegne grafen til T, og finner de to nullpunktene i definisjonsområdet: B=(5.8,0) og C=(8.9,0).

Temperaturen er over 0 grader Celsius fra 5,8 til 8,9 måneder etter 1. januar.

Mai: måned nr. 5. I tillegg 0,8*31 = ca. 25 døgn inn i mai (6 døgn igjen av mai). August: måned nr. 8. I tillegg 0,9*31 = ca. 28 døgn inn i august.

Til sammen er temperaturen over 0 grader Celsius: 6 døgn i mai + 30 døgn i juni + 31 døgn i juli + 28 døgn i august = 95 døgn.

b)

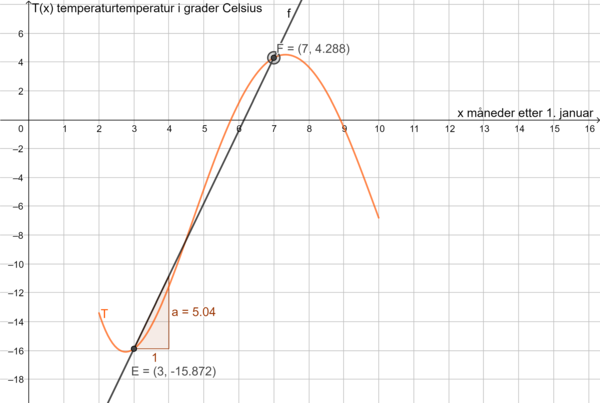
Lager punktene E=(3,T(3)) og F=(7,T(7)). Lager en linje mellom dem med knappen "linje", og finner stigningstallet til linjen med knappen "stigning".

Stigningstallet er 5.04, som betyr at temperaturen stiger med omtrent 5 grader Celsius per måned fra 1. mars til 1. juli.

Oppgave 2

Det er graf C som best beskriver lengden av turen som en funksjon av tiden.

Grafen må være en av dem som fortsetter å stige, fordi turen blir lengre og lengre etter hvert som Aurora går, uansett hvilken retning hun går i. Turen blir ikke kortere selv om hun snur og går hjem. Grafen kan derfor ikke gå nedover igjen.

Vi får vite at Aurora går med jevn fart, slik at grafen må ha jevn stigning når Aurora går (lineær).

I tillegg får vi vite at hun må stå i kø på postkontoret. Da er den en tid hvor lengden på turen ikke endrer seg.

Alle disse opplysningene passer med graf C.

Oppgave 3

a)

Dersom lengden er 60 meter, blir bredden 10 meter. Arealet blir da $60\cdot 10 = 600$ kvadratmeter.

b)

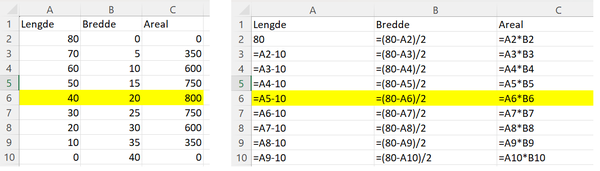
Bruker Excel til å lage en oversikt. Bildet viser oversikten til venstre, og formlene som er brukt til høyre.

Det kan se ut som om Herman sin påstand er riktig. I oversikten er det største arealet når lengden er dobbel så stor som bredden.

c)

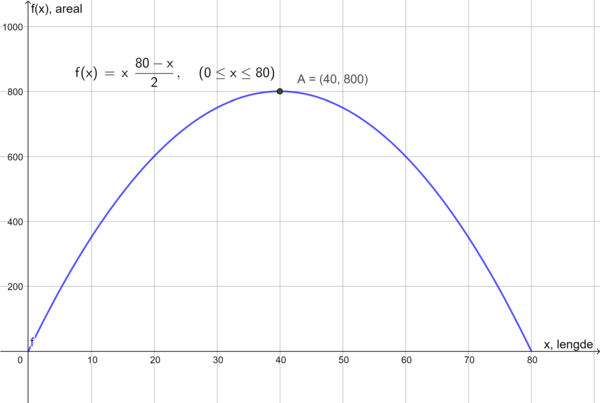
Funksjonen $f(x)=x\cdot \frac{80-x}{2}$ viser areal av rektangelet som funksjon av lengden x. Bruker Geogebra til å tegne grafen til f, og til å finne ekstremalpunktet A=(40,800).

Funksjonen viser at rektangelet har størst areal når lengden er 40, og da dobbelt så stor som bredden på 20.

Oppgave 4

a)

Sekk D er tyngst.

b)

Sekk A og C koster like mye.

c)

Sekk B har lavere vekt og lavere pris. Sekk C har omtrent dobbelt så stor vekt som B, men er ikke dobbelt så dyr. Det vil derfor være billigere kilopris på sekk C. Det lønner seg å kjøpe sekk C med tanke på kiloprisen.

d)

Sekk A og F koster like mye per kilogram, fordi man kan tegne en rett linje (lineær funksjon) gjennom origo, punkt A og punkt F. Det vil si at prisen og vekten er proporsjonale størrelser. pris = kg * pris/kg.

Oppgave 5

a)

Hver K øker med 4 non stop for hver figur (en ny non stop i hvert "hjørne").

Antall non stop i hver figur:

K1: 10

K2: 14

K3: 18

K4: 22

K5: 26

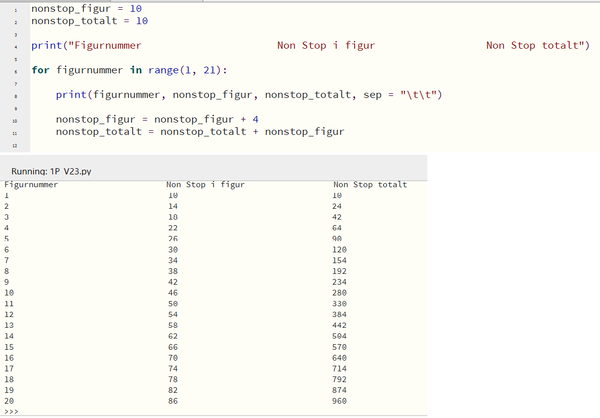
b)

c)

Kari trenger 960 Non Stop til sammen for å lage de 20 første figurene (se kjøring av programmet i oppgave b).

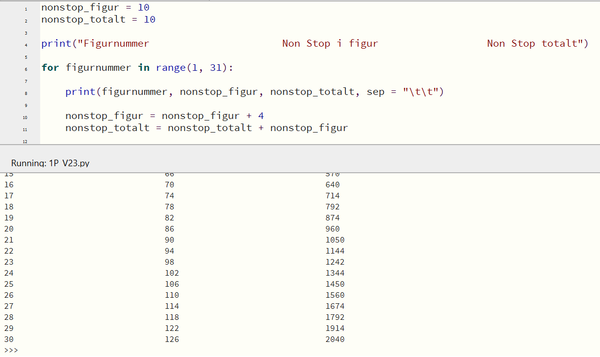
d)

Prøver meg frem, og endrer for-løkken til å kjøre litt flere ganger. Endrer til at løkken kjører 30 ganger, og ser at det tar 2040 Non Stop å lage 30 figurer. Det tar 1914 Non Stop å lage 29 figurer, så Kari kan lage 29 K-er med sine 2000 Non Stop.

Oppgave 6

a)

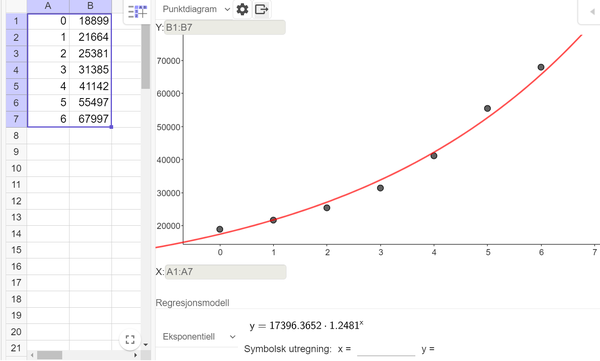
Bruker regresjonsanalyse i Geogebra til å finne en passende eksponentiell modell.

Modellen $E(x)=17396\cdot 1.248^x$ viser salg av antall tusen liter energidrikk i Norge x år etter 2015.

b)

Tallet a viser at det ble solgt 17296 tusen liter energidrikk i 2015, ifølge modellen (som ikke helt stemmer med dataene fra tabellen, som viser at det egentlig ble solgt 18899 tusen liter energidrikk i 2015).

Tallet b viser at den årlige vekstfaktoren er 1,248, som vil si at salget øker med 24,8 % årlig.

c)

Ifølge tabellen ble det solgt 67997 tusen liter energidrikk i 2021. Det ble solgt 73109 tusen liter i 2022. Det gir en økning på:

$\frac{73109-67997}{67997}\cdot 100 = 7,5$ %

Det er en mye mindre økning enn modellen tilsier. Modellen anslår en økning på 24,8 % årlig.