1P 2021 vår LK20 eksempel LØSNING 2

Oppgaven som pdf

Løsningsforslag laget av UDIR

Diskusjon av denne oppgaven

Oppgave 1

300 g koster 39kr. Ett gram koster 39 kr. : 300 = 0,13kr. 1000 gram koster da 0,13 gange 1000 som er 130 kr.

Oppgave 2

Grønne : $\frac {1}{10} = 10\%$

Røde : $\frac {3}{5} = \frac{6}{10} =60 \%$

Da er det 30% igjen som er gule.

Oppgave 3

1000 mg = 1 g

En tablett inneholder 600 mg omega-3. To tabletter inneholder 1200 mg som er 1,2 gram.

Oppgave 4

Mini vil koste 40 kroner, og Biggie vil koste 240 kroner.

Oppgave 5

$\frac{585}{1000} = \frac{58,5}{100} = 58,5 \%$

Oppgave 6

$M(x) = 0,075x + 32000$

$M(150 000) = 0,075 \cdot 150000 +32000 =43250$

Oppgave7

$ \frac{1,01417 \cdot 10^{13} }{5,372 \cdot 10^6} = 1,89 \cdot 10^6$

Oppgave 8

Hun har en fastlønn på 150 kr. Vi ser at grafen stiger med 150 når vi beveger oss 10 bøker bortover, det betyr at hun har 15 kr per bok. Hun må selge 20 bøker.

Oppgave 9

26 kg appelsiner krever $26 \cdot 5 = 130 $ dl sukker. Det er 13 liter og vekten er $ 13 \cdot 0,8 = 10,4$ kg. Hun trenger 11 pakker sukker.

Oppgave 10

a)

b)

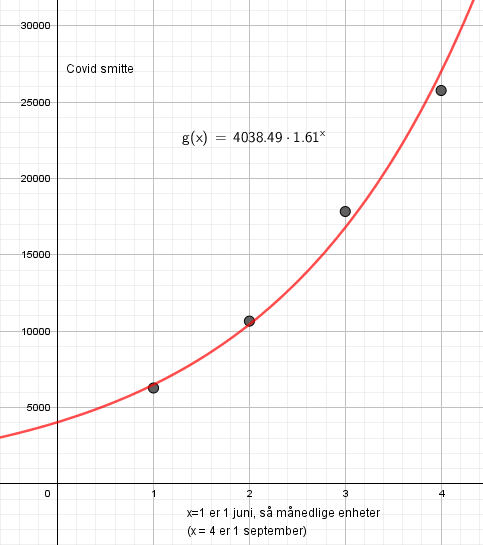
Økningen er på ca. 61% per måned i denne perioden.

Oppgave 11

a)

b)

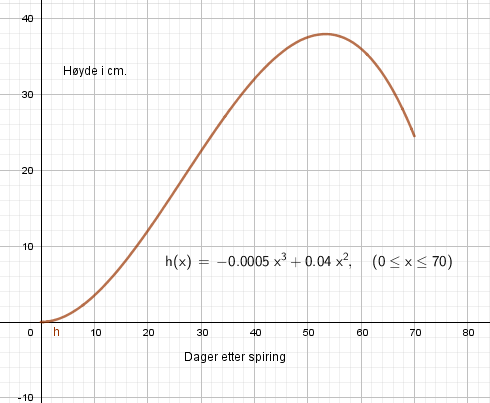
Modellen kan tenkes å være gyldig de første 50 dagene.

Oppgave 12

Oppgave 13

a)

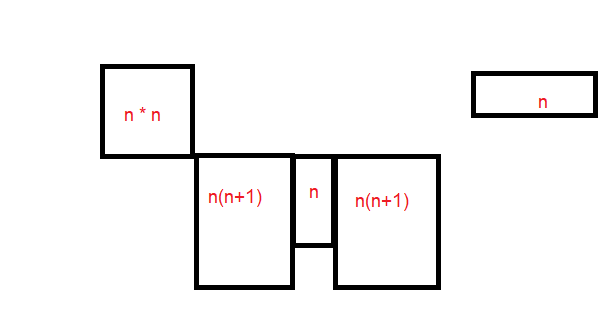
Ved å studere figurene ser man at de kan uttrykkes slik med figurnummeret n:

Antallet små kvadrater blir da: $A(n) = 3n^2 + 4 n$

b)

$A(100) = 3 \cdot 100^2 + 4 \cdot 100 = 30 400$

Oppgave 14

$ \frac{V_4}{V_2} = \frac{\frac 43 \pi(2r)^3}{\frac 43 \pi r^3} = 8 $

Når kulens radius dobbles, øker volumet med en faktor åtte.

Oppgave 15

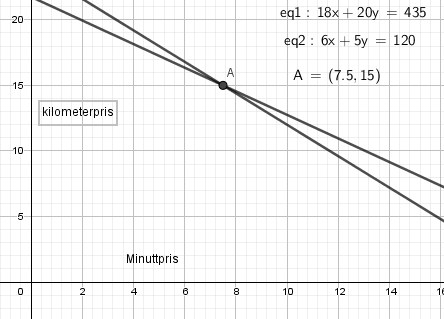
Taxi A tar en startpris på 75 kroner, i tillegg til en minuttpris på 7 kr / minutt og 14 kr / km.

Taxi B

Vi ser at prisen er kr 7,50 per minutt og 15 kr/km. I tillegg er startprisen kr 66.

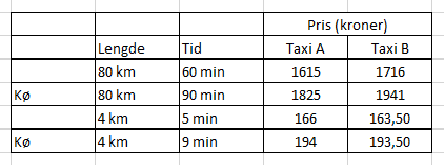
De ser ikke ut til å være stor prisforskjell på selskapene, men la oss sette opp fire senarioer. Langtur med og uten kø. Svipptur med og uten kø.

På korte turer er det i praksis liten forskjell, men på lengre turer er det litt å spare på å velge Taxi A.

Oppgave 16

Komfyren er ca 8,8 cm bred, der gryten står (perspektiv). Gryten er ca 2,6 cm bred. Diameter blir da:

$\frac{8,8}{2,6} =\frac{60}{x} $

x=18

Radius i gryten er ca 9 cm. Målt grytehøyde er ca 1,5 cm. Virkelig høyde blir da ca 10,5 cm.

Volumet av gryten blir ca 2,7 liter hvorav ca to liter inneholder saus. Dersom det ikke skal renne over har vi plass til ca. 0,6 liter kjøttboller. Hvor mange er det?

En kjøttbolle måler ca. 4 mm på bildet , dvs at den er ca. 2,7 cm i diameter (vi antar kuleform). Det gir en kjøttbolle et volum på $V= 4 \pi r^3 = 4 \cdot \pi \cdot (0,135dm)^3 = 0,03$ liter.

Ut fra forutsetningene gjort her er det plass til ca. 20 kjøttboller (0,6: 0,03=20).