1P 2021 vår K06 LØSNING

Eksamen 26.05.2021 MAT1011 Matematikk 1P. Kunnskapsløftet.

DEL EN

Oppgave 1

a)

Bruker Pytagoras og finner at avstanden AB er : $AB = \sqrt{300^2+400^2} = 500$ meter.

b)

$\frac{700-500}{500} = \frac 25 = 40$%. Sykkelturen er 40% lengre.

c)

Målestokk:

$\frac{4,0 cm}{0,8km} = \frac{4}{80000}= \frac{1}{20000}$

Målestokken er 1:20 000 som betyr at 1cm på kartet er 20 000 cm i virkeligheten, altså tilsvarer 1 cm på kartet 200 meter i virkeligheten.

Oppgave 2

$\frac{x}{80} = \frac{1200}{100}$

$ x = 12 \cdot 80 = 960$

Varen koster 960 kr, om den følger indeksen.

Oppgave 3

a)

Det koster 12 000 kroner.

Vi ser at to personer må betale 6000 kroner hver, eller at 4 personer betaler 3000 hver, osv.

b)

$x \cdot y = k$

Produktet av to omvendt proporsjonale størrelser er konstant. Nå x blir større, blir y mindre og motsatt. I dette eksempelet er k= 12 000 kr. I praksis betyr det at det blir billigere for den enkelte jo flere som er med på hytteturen.

c)

$y = \frac{12000}{x}$ Der y er prisen den enkelte betaler, og x er antall betalende personer.

Oppgave 4

Volum av boks: $V \approx 3 \cdot 25 \cdot 10 = 750$

Volumet av boksen er ca. 7,5 dl

Volumet av kaffe: $\frac{250}{35} = \frac{50}{7} = 7 + \frac 17$dl

Siden en syvendedel er mindre enn 0,5 får kaffen plass i boksen.

Oppgave 5

a)

I dette tilfelle er $x = \frac{40km/t}{10} = 4 $

Bremselengde ved 40 km/t =$ \frac{4^2}{2} = \frac{16}{2} = 8 $ m.

b)

Når farten øker til 80 km/t blir x = 8

Bruker samme formel og får $ \frac{8^2}{2} = \frac {64}{2} = 32$ som er fire ganger mere enn 8.

c)

På sommerføre ville en bil med fart 60 km/t hatt en bremselengde på 18 meter.

$\frac{72-18}{18} = \frac{54}{18} = 3$

Økningen i bremselengde er på 300%

Oppgave 6

a)

	Fornøyd	Ikke Fornøyd	Sum
VG 1	$48$	$72$	$120$
VG 3	$90$	$60$	$150$
Sum	$138$	$132$	$270$

b)

Tilfeldig elev fornøyd. $P(F) = \frac{130}{270} =0,5$

c)

VG 3 gitt fornøyd: $P(vg3 | fornøyd) = \frac{90}{138} \approx 0,65$, eller 65%.

Oppgave 7

a)

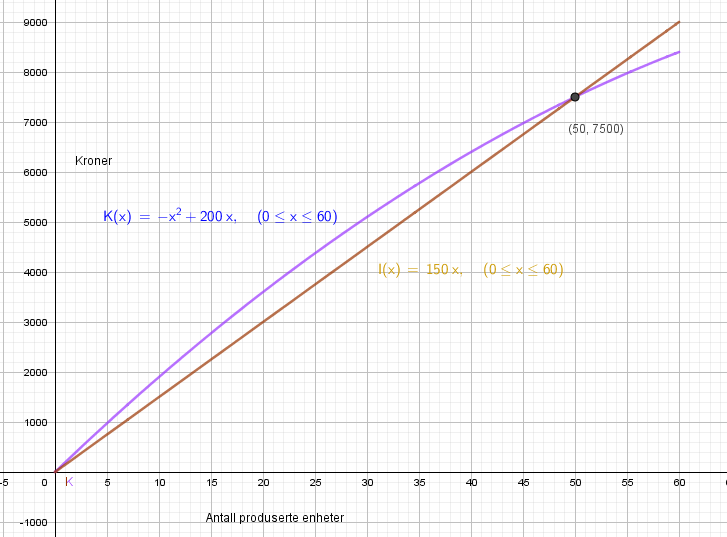
Vi sette x verdiene inn i uttrykket for K og får følgende tabell:

b)

c)

Fra figuren i b ser man at man må produsere 51 eller flere enheter før man får et overskudd.

DEL TO

Oppgave 1

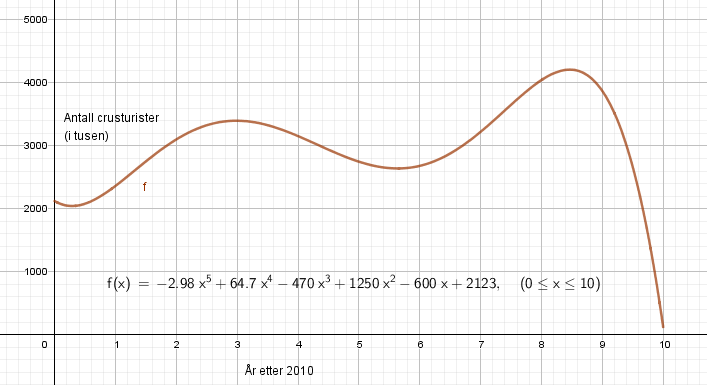
a)

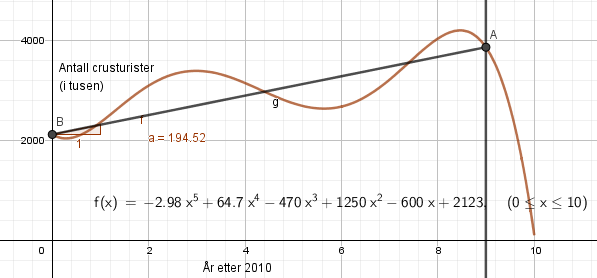
b)

Stigningstallet er 194,5. Det betyr at antall cruiseturister i perioden 2010-2019 økte i gjennomsnitt med ca. 194 500 per år.

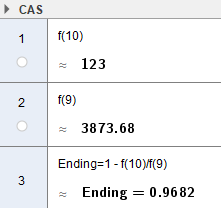
c)

Nedgangen var på nesten 97%.

Oppgave 2

a)

Når noe endrer seg lineært kan det skrives på formen y = ax + b.

Vi ser at på 5 år har innbyggertallet økt med 200. Det er en økning i snitt på 40 per år. Dersom vi lar x symboliserer år etter 2015 får vi

f(x) = 40x + 4600

Det som står under flekken er altså 40x.

b)

$f(15) = 40 \cdot 15 + 4600 = 5200$

Dersom modellen er god vil det være ca. 5200 innbyggere i bydelen i 2030.

Oppgave 3

Dersom han trekker uten tilbakelegging:

P(to av samme farge:) = P(to hvite) + P( to røde) =$\frac{6}{16} \cdot \frac{5}{15} + \frac{10}{16} \cdot \frac{9}{15} = \frac{24}{48} =0,5 $ = 50%

Vel dersom det er 50% sannsynlig at man trekker to drops med lik farge, må resten av mulighetene være ulik farge, altså 50% for det også.

Trekning med tilbakeligging:

P(to av samme farge:) = P(to hvite) + P( to røde) =$\frac{6}{16} \cdot \frac{6}{16} + \frac{10}{16} \cdot \frac{10}{16} = \frac{36+100}{256} =0,53 $ = 53%

Med tilbakelegging er ikke sannsynligheten for to like farger den samme som for to ulike farger. Detter er en svakhet med oppgaven og trekningsmetode burde vært presisert.

Oppgave 4

a)

En tomme = 2,54 cm

En lengde på 12,2 cm er da $\frac{12,2}{2,54} = 4,8$

Diagonalen er 4,8 tommer.

b)

Dersom forholdet er 16:9 mellom høyde og bredde, finner vi diagonalen ved Pytagoras, den blir 18,4 når forholdet mellom sidene er 16:9.

Vi vet at diagonalen er 12,2 cm og kan sette opp følgende forhold for å finne bredde og høyde:

$\frac{12,2}{18,4} = \frac{bredde}{9} \Rightarrow Bredde = 6 cm $

For å finne mobilens høyde bruker vi samme tankegang;

$\frac{12,2}{18,4} = \frac{høyde}{16} \Rightarrow Høyde = 10,6 cm $

c)

$\frac{(6,1)^2}{(4,8)^2} = \frac{37,21}{23,04}= 1,615$

Den nye telefonen har et areale som er 61,5% større enn den hun har nå.

Oppgave 5

a)

Rullen har form som en sylinder med radius 10 cm og høyde 80 cm. Vi må huske å trekke fra fra "sylinderen" som dannes av hullet i midten. $V = \pi r^2h $ som gir oss: $V_{papir} = \pi \cdot 10^2 \cdot 80 - \pi \cdot 0,7^2 \cdot 80 = 80 \pi(100 - 0,49) = 25,010 $. Vi har regnet i cm hele veien så $25010 cm^3 = 25,01dm^3$

b)

Når vi ruller ut papiret tenker vi at det har form som et prisme (boks) med en veldig liten høyde som tilsvarer tykkelsen på papiret.

$V = l \cdot b \cdot h \Rightarrow h = \frac{V}{l \cdot b} = \frac{25dm^3}{2500dm \cdot 8 dm} =0,00125 $ dm, som er 0,125 mm tykt.

c)

Papiret på rullen har en flate på $A = l \cdot b = 250 m \cdot 0,8 m = 200 m^2$

Da blir massen av papir $200m^2 \cdot 60 g/m^2 = 12000g = 12 kg$

Oppgave 6

a)

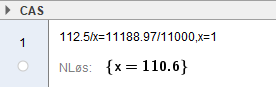
Indeksen var 110,6 i 2019.

b)

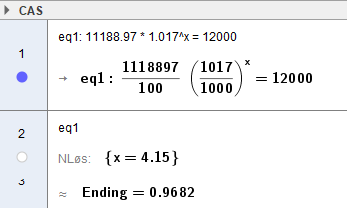
Den vil tidligst passere 12 000 kr. i august 2025.

Oppgave 7

a)

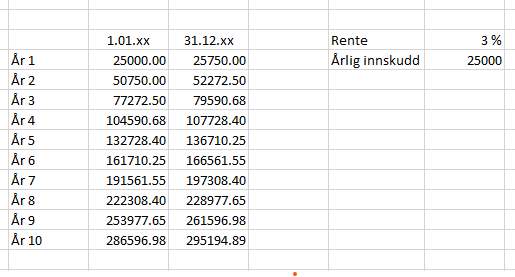
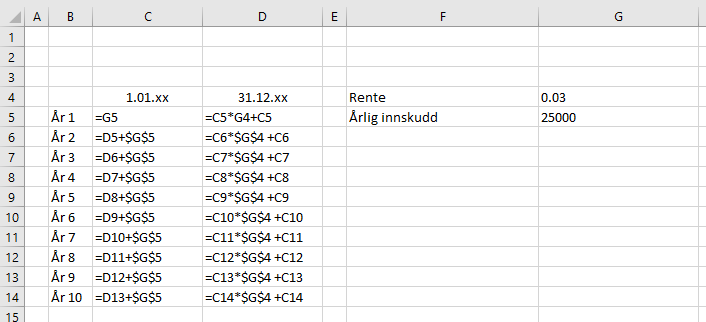
Man kan totalt sette inn 300 000 kr, og maksimum 25 000 kroner per år. Dersom hun setter inn 25 000 kroner årlig blir det 12 år. Det betyr at hun må senest starte når hun er 22 år gammel, i 2024.

b)

Det største skattefradraget man kan få er 20% av 300 000 kr, altså 60 000 kroner fordelt over minimum 12 år.