1P 2021 høst LK20 LØSNING
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
DEL EN
Oppgave 1
Det betyr at 5 elever utgjør 20%, Da er 25 elever 100%.
Oppgave 2
Grunnlaget man regner prosenten fra forandrer seg hvert år. Du kan sette opp stykket slik:
$x \cdot 0,90^3 = 400 000 $
$x = 400 000 \cdot 0,90^{-3} $
Oppgave 3
a)
$T = 9t + 7$
$52 = 9 t + 7$
$9t = 45$
$t = 5$
Det tar ca. fem timer.
b)
7 er starttemperaturen ved tiden t = 0. 9 er antall grader temperaturen stiger med hver time.
Oppgave 4
Han bruker 9 minutter på første delen og 12 minutter på siste halvdel, totalt 21 minutter:
$\frac{12}{80} timer \cdot 60 + \frac {12}{60} timer \cdot 60 = 9 + 12 $ minutter
Oppgave 5
a)
f(x) vi ser at grafen krysser y aksen i 3 og at stigningstallet er -2 (to til høyre og fire ned). Det gir f(x) = -2x + 3
g(x) = 1/2 x - 2 ( stigningstall: to til høyre og en opp (delta y delt på delta x)
b)
Høyden i trekanten er 1. Grunnlinjen er : g(x)=0 gir x = 4, og f(x)= 0 gir x = 1,5. Grunnlinjen G= 4 - 1,5 = 2,5. Arealet blir halvparten av G*h som er 1,25.
DEL TO
Oppgave 1
a)
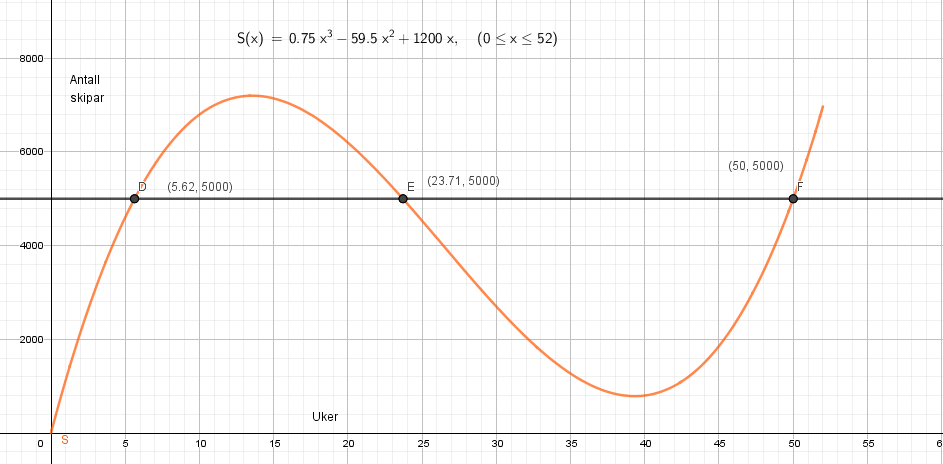
Tegner grafen til funksjonen S i Geogebra. Lager linja y=5000 og finner skjæringspunktene mellom linja og grafen til S. Ser at butikken kan selge mer enn 5000 par ski fra uke 5.6 til uke 23.7 (litt over 18 uker), og fra uke 50 til 52 (2 uker). Det vil si at butikken kan selge mer enn 5000 par ski i ca. 20 uker, ifølge modellen.
b)
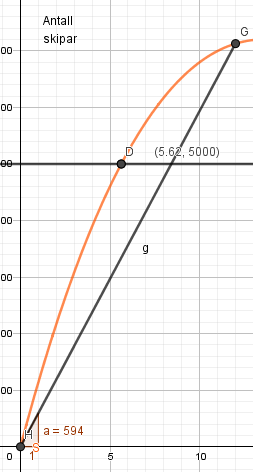
Stigningstallet er 594, det betyr at i årets første 12 uker øker skisalget i gjennomsnitt med ca. 600 par i uken.
Oppgave 2
a)
Energiinnhold i 100 gram kokt egg:
Energi fra fett + energi fra protein + energi fra karbohydrater = $(9 \cdot 10,2 + 4 \cdot 12,4 + 4 \cdot 0,3) kcal = 142,6 kcal$
b)
Gram spiselig: $125g \cdot 0,88 = 110g $
Energi: $1,1 \cdot 142,6 = 156 kcal $
Hvilket utgjør ca 5 % av dagsbehovet.
Oppgave 3
a)
Dersom en bestand bestående av 500 dyr dobler seg lineært på 10 år ser funksjonen slik ut: L(x) = 50 x + 500
b)
Dersom bestanden øker eksponentielt får vi:
$E(x)= 500 \cdot 1,07^x$
c)
d)
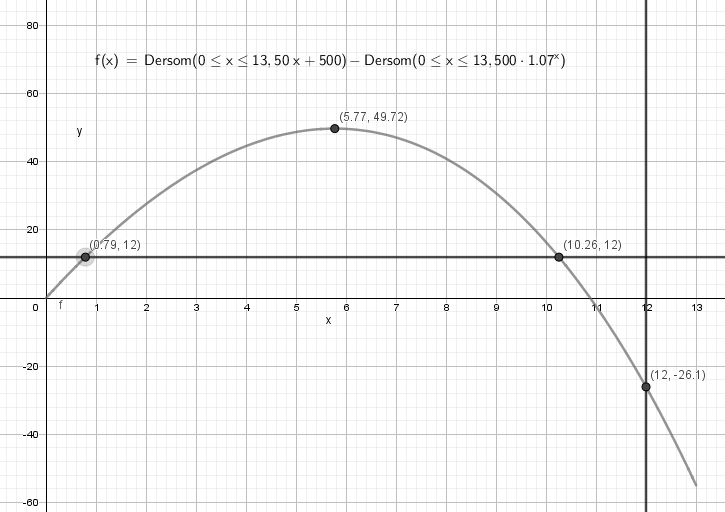
Grafen til f viser forskjellen i estimat mellom den lineære modellen og den eksponentielle, under de gitte forutsetninger. Den største forskjellen er på ca. 50 dyr, etter ca 6 år. Den praktiske tolkningen av y= 12 er ved hvilke tidspunkt den lineære modellen estimerer 12 dyr mer enn den eksponentielle. For x = 12 får vi en funksjonsverdi nær - 26. Det må tolkes som at den eksponentielle funksjonen nå har det høyeste estimatet, og etter 12 år viser den eksponentielle funksjonen ca. 26 dyr mer enn den lineære funksjonen.
Begge funksjonene, L og E skulle doble seg på 10 år. Fra figuren i c ser man at det tar nesten 11 år før E dobler seg. Det skyldes at jeg burde tatt med en desimal til i uttrykket for vekstfaktoren.
Oppgave 4
Påstand 1 er riktig: $pris per elev =\frac{totalutgift}{Antallelever}$
Påstand 2 er feil: $x$ og $x^2$ er eksempler på størrelser der dersom x øker så øker kvadratet av x også, men de er ikke propirsjonale.
Påstand 3 er riktig: $y = \frac kx$, om vi dobler x : $y = \frac {k}{2x}$, halveres y.
Påstand 4 er feil: Forholdet mellom areal og omkrets vil være: $\frac A O = \frac{\pi r^2}{s \pi r} = \frac {r}{2}$. Dette forholdet er ikke konstant, men varierer med r. Derfor ikke proporsjonalitet.
Oppgave 5
Saftblandingen består av 1 del sukker og ni deler ikke sukker. Dersom mengden sukker økes med 50% betyr det at vi har 1,5 del sukker og 9 deler ikke sukker. Det er totalt 10,5 deler. $\frac{1,5}{10,5} = 14,3$. Den nye blandingen vil inneholde i overkant av 14% sukker.
Oppgave 6
a)
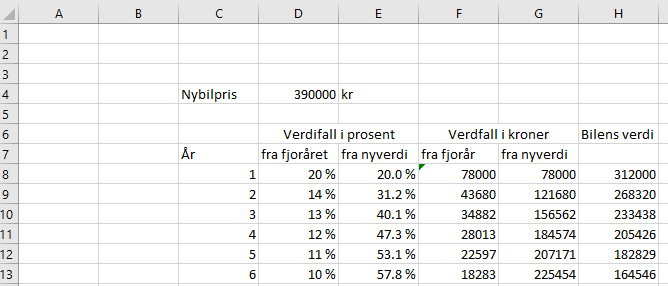
Ett verdifall på 20 % gir en vekstfaktor på 0,8. Et videre fall på 14 % gir et totalt fall på $0,8 \cdot 0,86 = 0,688.$ 1 - 0.688 = 0,312 = 31%.
b)
c)
Se figur i b.
Oppgave 7
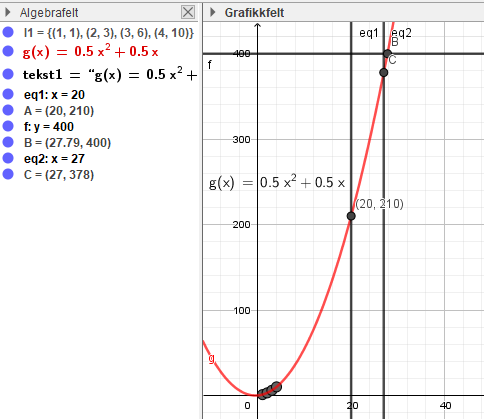
a)
Finner funksjonsuttrykket ved regresjon i Geogebra. Lager linja x = 20 og bruker "skjæring mellom to objekt" mellom denne linja og polynomfunksjonen.
Ser at 20 etasjer krever 210 bokser, se punkt A.
b)
Skriver y=400 og bruker "skjæring mellom to objekt" mellom denne linja og polynomfunksjonen.
Marius kan lage maksimalt 27 etasjer med 400 bokser, se punkt B i oppgave a). Til det trenger han 378 bokser, se punkt C i oppgave a).
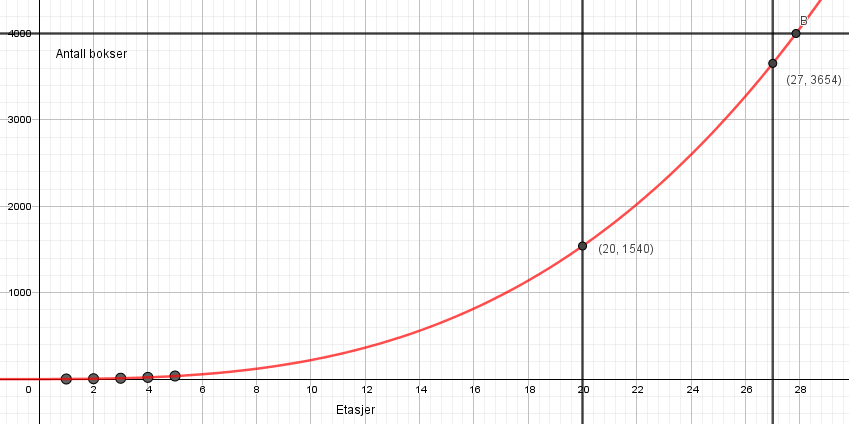
c)
Bruker polynomregresjon av 3. grad:
Lager linja x = 20 og bruker "skjæring mellom to objekt" mellom denne linja og polynomfunksjonen.
20 etasjer krever 1540 bokser. Se figur.
d)
Skriver y=4000 og bruker "skjæring mellom to objekt" mellom denne linja og polynomfunksjonen.
Det er 27 etasjer i det største tårnet Maria kan lage med 4000 bokser, se figuren i c.
Oppgave 8
a)
Tallene er organisert i et kvadrat med tall fra 1 til 100, ti bortover og ti nedover. Et tilfeldig valgt tall n som ikke ligger på randen av det store kvadratet vil ha naboen n+1 til høyre for seg, og n-1 til venstre. Rett ned ligger n + 10 og rett opp n-10.
differansen en opp og en til høyre blir 11 - 2 = 9 (blått kvadrat) eller 37 - 28 = 9 (rød kvadrat). Den andre diagonalen får verdi 11 og produktet av 11 og 9 er 99, samme for både blått og rødt kvadrat.
b)
Uansett valg av 2 x 2 kvadrat blir produktet 99. Årsaken er at det kvadratet du velger har tallene : 
Differansen i diagonalen opp mot høyre vil være (n + 10) - (n + 1) = 10- 1 = 9 . Den andre diagonalen får differanse (n + 10 + 1) - n = 11
c)
Ett 3 x 3 kvadrat har alltid verdiene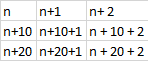 
Produktet vil alltid være $18 \cdot 22$