1P 2018 høst LØSNING
Diskusjon av denne oppgaven på matteprat
Løsning som pdf laget av Marius Nilsen ved Bergen private gymnas
DEL EN
Oppgave 1
20 tulipaner
Hvite 25%: $20 \cdot \frac 14 $ = 5 stk.
Gule: $20 \cdot \frac 15 =4 stk $
Røde tulipaner: 20 - 5- 4 = 11 tulipaner.
Oppgave 2
| 2015 | 2017 | |
| KPI | 100 | 105,5 |
| Pris | 400 | x |
$\frac{100}{400} = \frac{105,5}{x} \\ 100x = 105,5 \cdot 400 \\ x = \frac{105,5 \cdot 400}{100} \\ x = 105,5 \cdot 4 \\ x = 422$
Pris i 2017 er kr. 422.
Oppgave 3
a)
Dersom pris per pakke delt på antall griser er den samme i alle tilfellene er antall griser og pris proporsjonale.
$72 :3 = 24 \\ 120:5 =24 \\ 180:8 = 22,5$
Dette er IKKE proporsjonale størrelser.
b)
$\frac{melis}{mandler} = \frac{3}{2} = \frac{x}{700\, g} \\ 2x = 2100 \, g \\ x = 1050 \, g $
De trenger 1050 g melis til 700 g mandler.
c)
Når blandingsforholdet er 2 deler til 3 deler, er det totalt 5 deler.
$7,5 : 5 = 1,5 \, $
En del tilsvarer 1,5 kg.
Det er 3 kg mandler og 4,5 kg melis i blandingen.
Oppgave 4
a)
Vi får informasjon om at hypotenusen er 10 cm lang, og det lengste kateter er 8 cm.
Areal av mindste kvadrat:
$A = 100 \, cm^2 - 64 \, cm^2 = 36 \, cm^2$
b)
Lengde av korteste side:
$K_k = \sqrt{100 \, cm^2 - 64 \, cm^2} = 6$ cm
Oppgave 5
a)
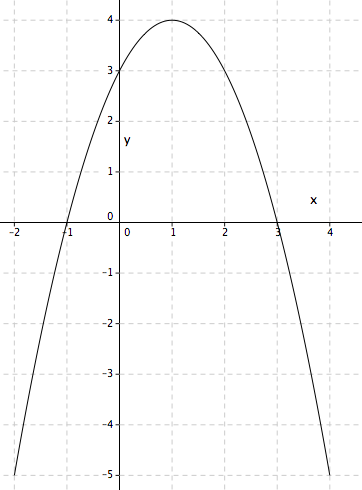
| x | (-2) | (-1) | 0 | 1 | 2 | 3 | 4 |
| f(x) | (-5) | 0 | 3 | 4 | 3 | 0 | (-5) |
b)
Oppgave 6
a)
20 cm : 100 m=
20 cm : 10000 cm =
2: 1000=
1:500
b)
$\frac{x}{6900} = \frac{1}{500} \\ 500x = 6900 \\ x= 13,8 $
Modellens bredde er 13,8 cm.
Oppgave 7
a)
Følgende fem kombinasjoner gir summen åtte:
$ U= \{ (2,6), (6,2), (3,5), (5,3), (4,4) \} $
I tre av tilfellene viser ingen av terningene en toer.
$P(ingen \, toer)= \frac{3}{5}$
Sannsynligheten for at ingen av terningene viser en toer er $ \frac{3}{5}$.
b)
Følgende ti kombinasjoner gir nøyaktig én toer:
$U= \{ (2,1), (2,3), (2,4), (2,5), (2,6), (1,2), (3,2), (4,2), (5,2), (6,2) \} $
Totalt er det $6 \cdot 6=36$ mulige kombinasjoner for ett terningkast med to terninger.
$ P(nøyaktig \, én \, toer)=\frac{10}{36}= \frac{5}{18} $
Sannsynligheten for å få nøyaktig én toer er $\frac{5}{18}$.
Oppgave 8
a)
Avdrag pluss restlån første året blir 200 000 kroner, som var det han lånte.
b)
Han betaler 6000 kroner av 200 000 kroner. Det er $\frac{6000}{200 000} = \frac{6}{200} = \frac{3}{100}= 3$ %.
c)
Terminbeløpet er det samme hvert år, altså er dette et annuitetslån.
DEL TO
Oppgave 1
a)
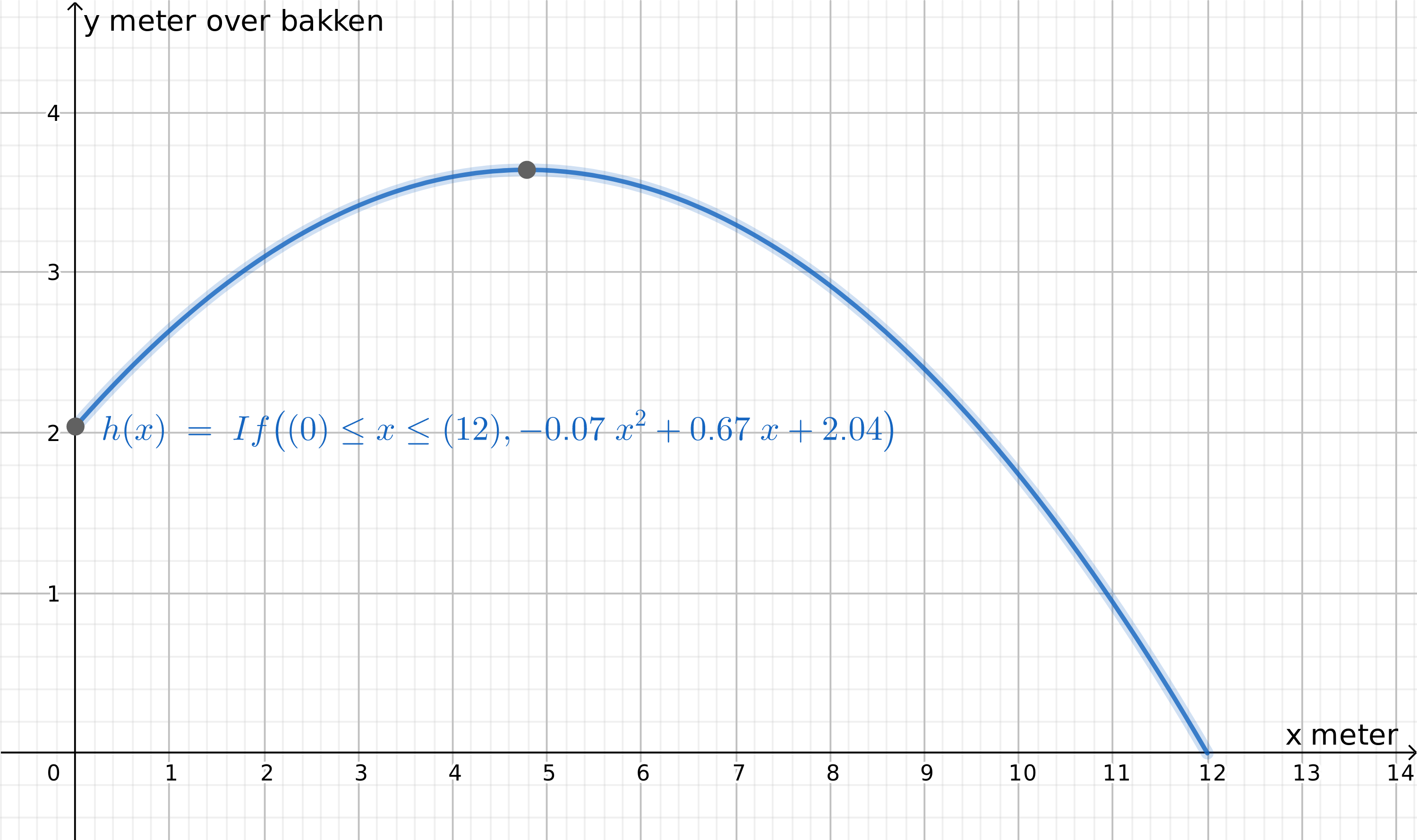
Ballen er da 2,04 meter over bakken (x = 0)
b)
c)
Bruker kommandoen "Ekstremalpunkt" og finner at ballen er 3,64 meter på det høyeste.
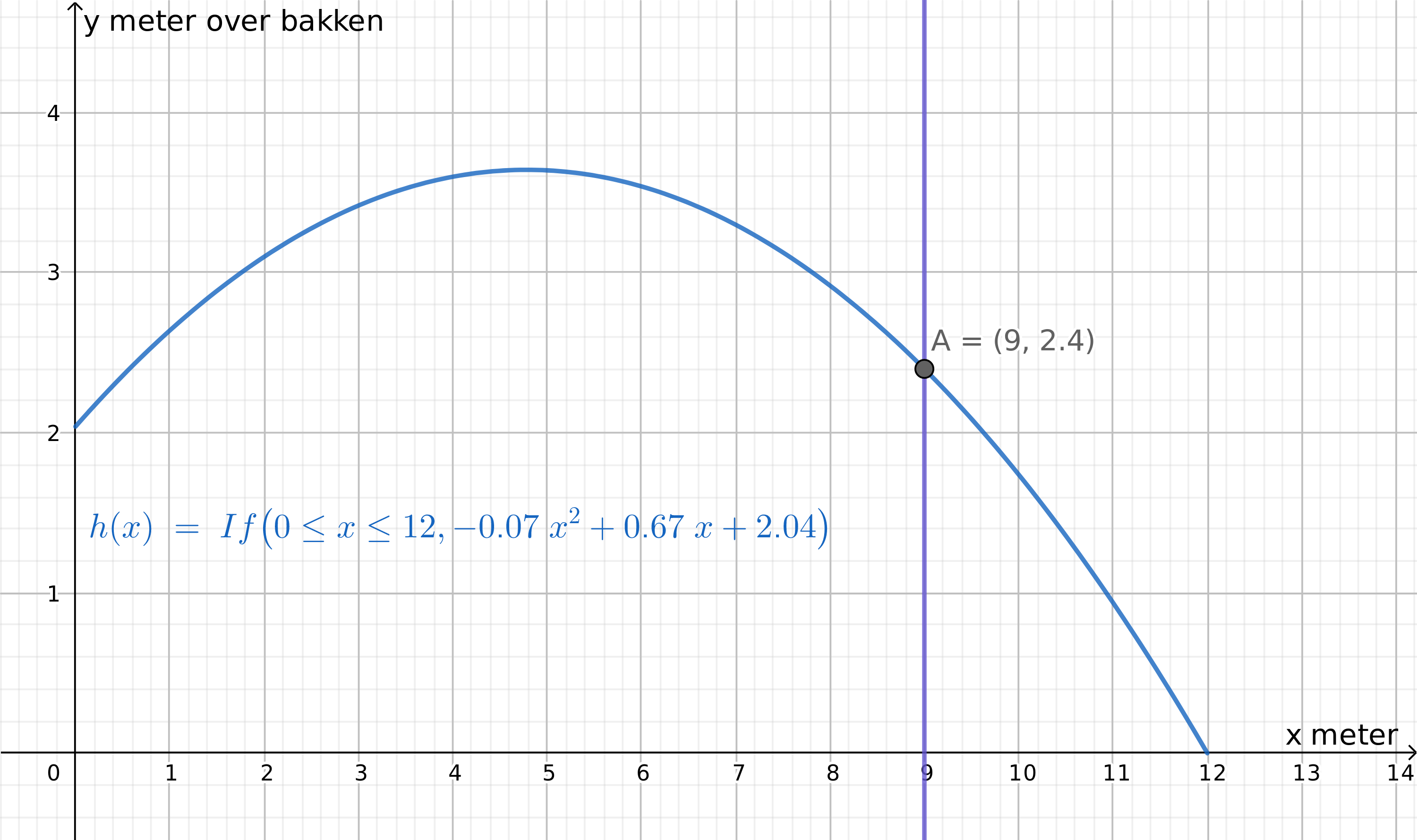
d)
Nettet står midt på banen, 9 meter fra enden av banen på hver side. Lager linjen x=9, som representerer der hvor nettet står, og finner skjæringspunktet mellom linja og grafen til h. Vi ser av punkt A at etter 9 meter, er ballen 2,4 meter over bakken.
For en kvinne som slår ballen fra banens ende, vil ballen gå over nettet (som er 2,24 meter høyt).
For en mann som slår ballen fra banens ende, vil ballen akkurat ikke gå over nettet (som er 2,43 meter høyt). Hvis mannen går litt frem, vil ballen kunne gå over nettet.
Oppgave 2
a)
Krysstabell:
| Kjøpte popcorn | Kjøpe ikke popcorn | Sum | |
| Kjøpte smågodt | 80 | 140 | 220 |
| Kjøpte ikke smågodt | 200 | 30 | 230 |
| Sum | 280 | 170 | 450 |
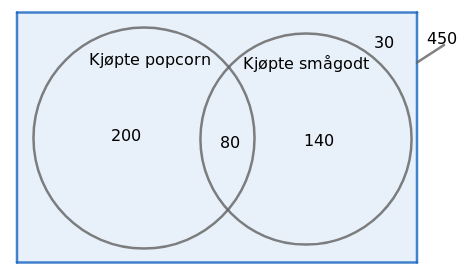
Venndiagram:
b)
$P(popcorn \cap smågodt) = \frac{80}{450} \approx 0,178 = 17,8% $
Sannsynligheten for at en tilfeldig valgt kunde kjøpte både popcorn og smågodt er ca. 17,8%.
c)
$P(ikke\,popcorn | smågodt) = \frac{140}{220} \approx 0,636 = 63,6% $
Sannsynligheten for at kunden som kjøpte smågodt, ikke kjøpte popcorn, er ca. 63,6%.
Oppgave 3
Volum av kule med radius r: $V_{kule}= \frac 43 \pi \cdot r^3$
Volum av kjegle med radius og høyde lik r: $V_{kjegle} = \frac{1}{3} \pi \cdot r^2 \cdot h = \frac{1}{3} \pi \cdot r^2 \cdot h = \frac{1}{3} \pi \cdot r^3$
Volum av sylinder med radius og høyde lik r: $V_{sylinder} = \pi \cdot r^2 \cdot h = \pi \cdot r^2 \cdot r = \pi r^3$
$V_{kjegle} + V_{sylinder} =\frac{1}{3} \pi \cdot r^3 + \pi \cdot r^2 \cdot r = \pi r^3 =\frac 43 \pi \cdot r^3 =V_{kule}$
Vi har vist at det gjelder generelle. Dersom du setter inn 4 alle steder for r og h ser du at summen av volumene for kjegle og sylinder er lik det for kulen.
Oppgave 4
Sider i trekanten: 6, 10 og 14.
$s = \frac{6+10+14}{2}= 15$
$T = \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{15 \cdot 9 \cdot 5 \cdot 1} = 25,98 \approx 26$
Oppgave 5
a)
Bruker formelen $a=\frac{y_2 - y_1}{x_2 - x_1}$
$a=\frac{102,9 \, kW-80,85 \, kW}{140 \, hk-110 \, hk}=\frac{22,05 \, kW}{30 \, hk}=0,735 \, \frac{kW}{hk}$
Stigningstallet er 0,735 kW/hk.
b)
$1000 \, hk \cdot 0,735\frac{kW}{hk} = 735 \, kW$
1000 hk tilsvarer 735 kilowatt.
Oppgave 6
a)
2014: KPI= 97,9 Lønn 550 000 kr.
Reallønn =Lønn $ \cdot \frac{100}{KPI} = 550000kr \cdot 1,02145=561798 kr$
b)
Lønn $ \cdot \frac{100}{105,5} =561798 kr \\ Lønn = 592697 kr$
Oppgave 7
a)
To trekanter er formlike dersom de har to parvis like store vinkler.
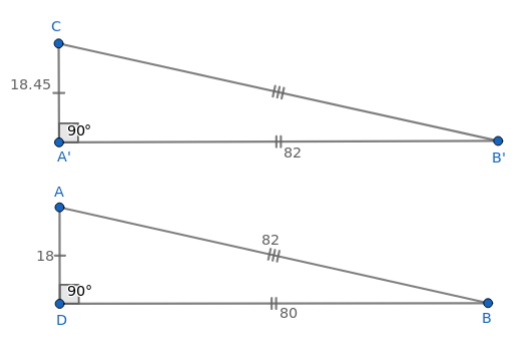
$\triangle ABC$ har en rett vinkel i $\angle A$, og $\triangle ABD$ har en rett vinkel i $\angle D$.
$\angle B$ er felles for $\triangle ABC$ og $\triangle ABD$.
Trekantene har to parvis like store vinkler, og er derfor formlike.
b)
Vi vet at AD = 18 km og BD = 80 km. Vi bruker Pytagorassetningen for å finne lengden til AB.
$(AB)²=(AD)²+(BD)² \\ AB=\sqrt{18²+80²} \\ AB=82$
Bruker formlikhet for å finne lengden til AC.
$\frac{AC}{AD}=\frac{AB}{BD} \\ \frac{AC}{18} = \frac{82}{80} \\ AC=\frac{82}{80} \cdot 18 \\ AC = 18,45$
Det er 18,45 km fra A til C.
Oppgave 8
a)
Pris en skjorte = p
Ordinær pris er 2p, han betaler 1,5p. Rabatt: $\frac{0,5p}{2p} =\frac{0,5 \cdot 50 }{2 \cdot 50} =\frac{25}{100}= 25$%
b)
Den billigste skjorta koster x kroner, og den dyre koster (x + 300). Han betaler bare for halvparten av den billigste:
$\frac x2 + (x + 300) = 1350 \\ \frac 32x = 1050 \\ 3x= 2100 \\ x= 700$
Han betalte halvparten av 700 kr, altså 350 kr.
Oppgave 9
a)
Bruker programmet LibreOffice Calc, som stort sett er likt Excel.
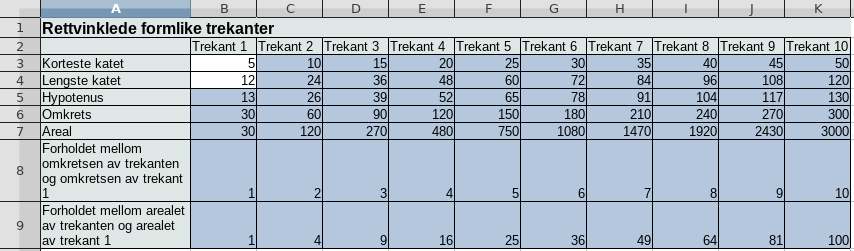
Uten formler:
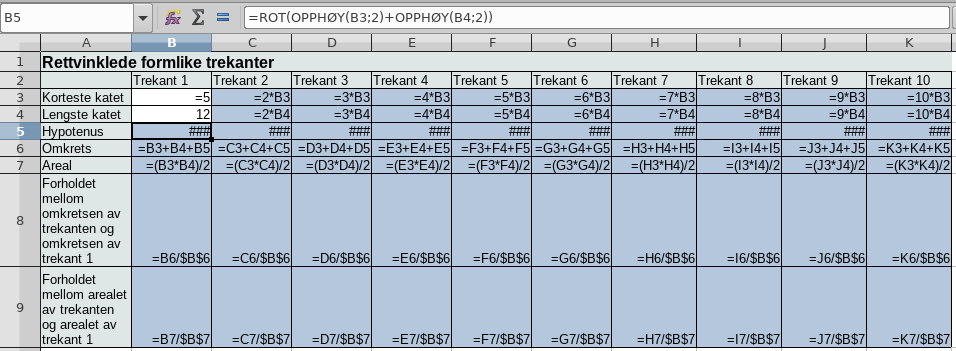
Med formler:
Se i skrivefeltet (øverst i skjermbildet) for formelen for hypotenus. Denne formelen vil være litt annerledes i Excel.
b)
For hver trekant er tallet i rad 9 kvadratet av tallet i rad 8.
c)
Tallene i rad 8 og rad 9 vil ikke endre seg om du endrer tallene i celle B3 og celle B4, som er lengden til katetene i trekant 1.
Dersom du endrer lengden til katetene i trekant 1, vil fremdeles sidene i trekant 2 være dobbelt så lange som i trekant 1, sidene i trekant 3 være tre ganger så lange som i trekant 1, og så videre. Alle trekantene vil fremdeles være formlike rettvinklede trekanter, og dermed vil forholdet mellom arealet til trekantene være det samme som før. Det samme gjelder forholdet mellom omkretsen til trekantene.